前回の記事([NumPy]FFTでフィルタリング ①フーリエ級数展開と離散フーリエ変換)では、NumPyのFFTの結果のうち、周波数を見てきました。
今回は、FFTで得られたフーリエスペクトル(複素数)について見ていきたいと思います。
前回は単一周期のサイン波を対象にしましたが、フーリエ級数展開を意識して直流成分を含んだ複数周期&複数位相からなる信号を対象にしてみます。
$$ f(t) = 0.5 + sin(2πt) + cos(4πt) + sin(6πt) $$
フーリエ級数展開の式に当てはめるとこのように表せます。
$$ f(t) = \frac{a_{0}}{2}+\sum_{m=1}^{3}[a_{m}cos(2πmt)+b_{m}sin(2πmt)] $$
| \(m[Hz]\) | \(a_m\) | \(b_m\) |
|---|---|---|
| 0 | 1 | – |
| 1 | 1 | 0 |
| 2 | 0 | 1 |
| 3 | 1 | 0 |
この関数を、データ長:\(N=10000\)、サンプリング周波数:\(f_{s}=100[Hz]\)として離散化して、下記のPythonコードで離散フーリエ変換をしてみたいと思います。データ長は対象とする信号の周期よりも十分長いものとしました。
前回と同じく、できるだけ本文中の記号と、コード中の変数名を合わせようとしていますが、限界があったり、(個人的な)可読性の面から敢えて変えているところも多い点をご容赦ください。
import os import numpy as np #### 関数 #### # シグナル生成(F:周波数, AS:振幅(sin), AC:振幅(cos), fs:サンプリング周波数, Length:信号長) def GenSignal(F, AS, AC, fs, Length): Ts = np.arange(0, Length * 1/fs, 1/fs) return AS * np.sin(F*Ts*2*np.pi) + AC * np.cos(F*Ts*2*np.pi) #### 設定事項 #### N = 10000 #データ長 FS = 100 # サンプリング周波数[Hz] FF = [1, 2, 3] # 信号の周波数[Hz] AS = [1, 0, 1] # 振幅_SIN[A.U.] AC = [0, 1, 0] # 振幅_COS[A.U.] CONST = 0.5 #直流成分 #### 設定ここまで #### #シグナル生成(FF:周波数, AS:振幅(Sin), AC:振幅(Cos), fs:サンプリング周波数, Length:信号長) signal = np.repeat(CONST, N) for i in range(len(FF)): signal += GenSignal(FF[i], AS[i], AC[i], FS, N) #周波数:1Hz、サンプリング周波数:100Hz、信号長:N) #周波数領域に変換 signal_f = np.fft.fft(signal) freqs = np.fft.fftfreq(N, d=1.0/FS)
色々と設定が長くなっていますが、実際のフーリエ変換(FFT)は最後から2行目のnp.fft.fftのところです。また、変数freqsに周波数の一覧が格納されています。
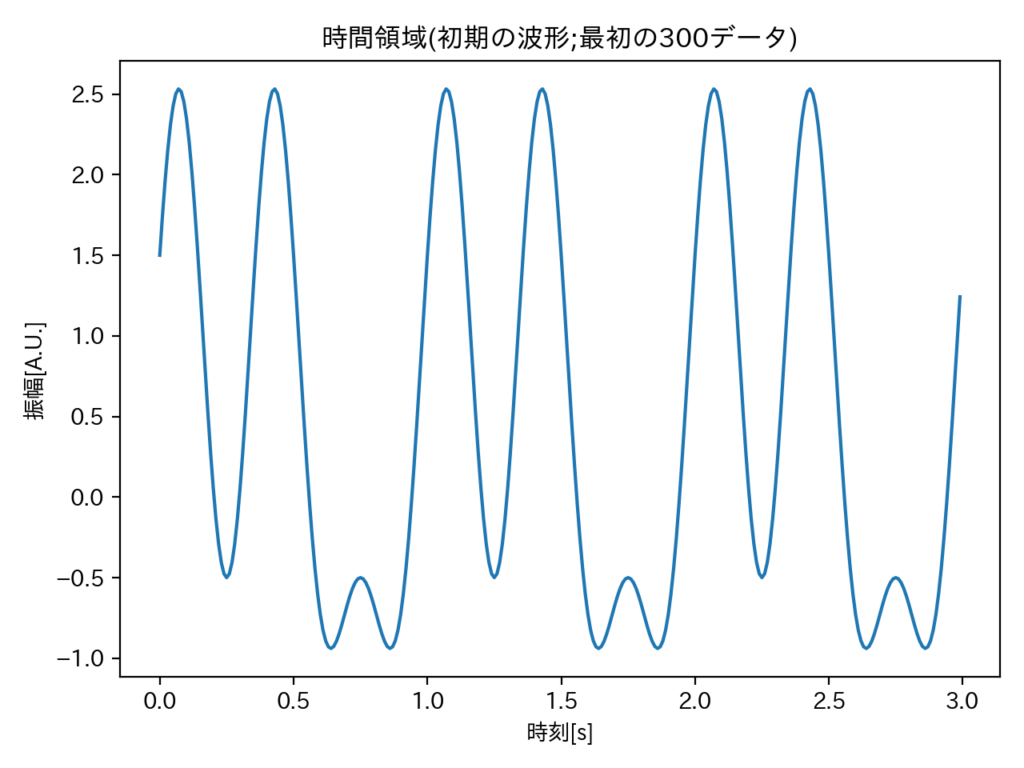
ちなみに、\(f(t)\):変数名signalを絵に描くとこんな形になります。
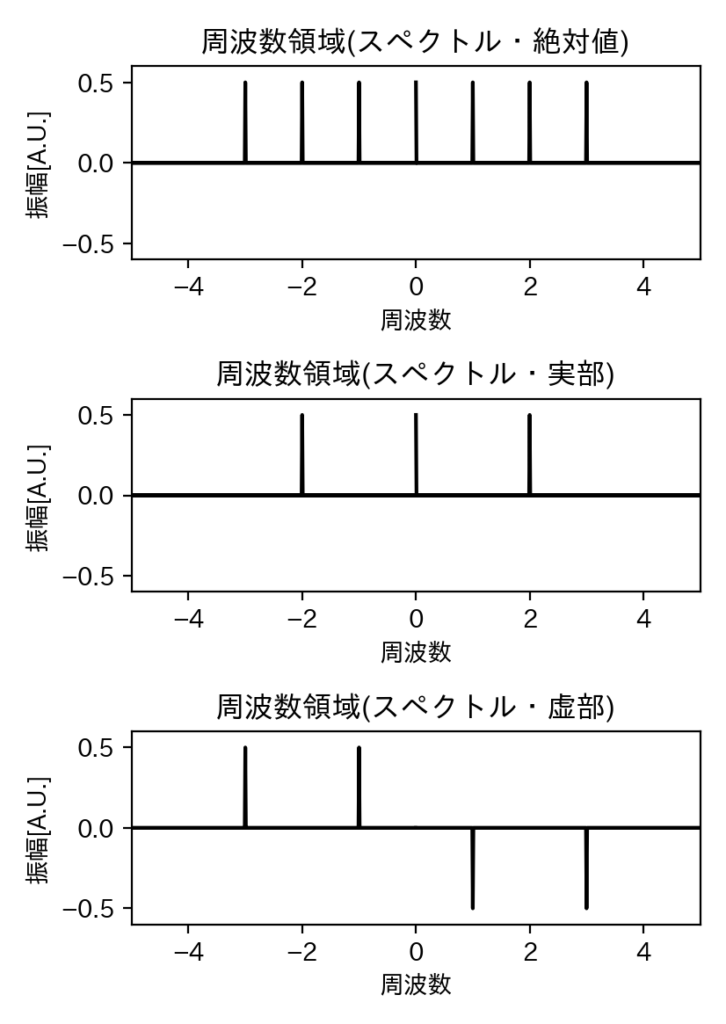
さて、FFTの結果(変数:signal_f)は複素数の配列となっており、絶対値・実部・虚部の振幅スペクトルを描くと下記のようになります。
最上段の絶対値を見ると、直流成分(0Hz)、±1Hz、±2Hz、±3Hzのところにスペクトルが立っています。
中段の実部を見ると、直流成分(0Hz)、±2Hzの3本のスペクトルが立っています。
下段の虚部を見ると、-1Hzと-3Hzに正の値、+1Hzと+3Hzに負の値のスペクトルが立っています。虚部のスペクトルは周波数が正負で共役の複素数となっていることがわかります。
なお、振幅スペクトルを描くに当たっては、データ数(N)で除しています。
直流成分の振幅は0.5\(=\frac{a_0}{2}\)とフーリエ級数展開の振幅と一致しています。一方で交流成分の振幅も0.5と合ってないように思われますが、正の周波数と負の周波数を合わせると振幅は1.0となります。
離散フーリエ変換の結果を\(X(f_k)\)(Pythonコード中の変数名:signal_f)としたうえで、\(X(f_k)=α_k+β_k i\)(α・βは実数)とすると、主な結果は下記の通りとなります。なお、\(N=10000\)(データ長)となります。
| k | freqs[k] | \(f_k\) | \(α_k\) | \(β_k\) |
|---|---|---|---|---|
| 0 | 0.00 | \(\frac{kf_s}{N}\) | 0.5×N | 0 |
| 1 | 0.01 | \(\frac{kf_s}{N}\) | 0 | 0 |
| ・・・ | ||||
| 99 | 0.99 | \(\frac{kf_s}{N}\) | 0 | 0 |
| 100 | 1.00 | \(\frac{kf_s}{N}\) | 0 | -0.5×N |
| 101 | 1.01 | \(\frac{kf_s}{N}\) | 0 | 0 |
| ・・・ | ||||
| 199 | 1.99 | \(\frac{kf_s}{N}\) | 0 | 0 |
| 200 | 2.00 | \(\frac{kf_s}{N}\) | 0.5×N | 0 |
| 201 | 2.01 | \(\frac{kf_s}{N}\) | 0 | 0 |
| ・・・ | ||||
| 299 | 2.99 | \(\frac{kf_s}{N}\) | 0 | 0 |
| 300 | 3.00 | \(\frac{kf_s}{N}\) | 0 | -0.5×N |
| 301 | 3.01 | \(\frac{kf_s}{N}\) | 0 | 0 |
| ・・・ | ||||
| 4999\((\frac{N}{2}-1)\) | 49.99 | \(\frac{kf_s}{N}\) | 0 | 0 |
| 5000\((\frac{N}{2})\) | -50.0 | \(\frac{kf_s}{N}-{f_s}\) | 0 | 0 |
| 5001\((\frac{N}{2}+1)\) | -49.99 | \(\frac{kf_s}{N}-{f_s}\) | 0 | 0 |
| 5002\((\frac{N}{2}+2)\) | -49.98 | \(\frac{kf_s}{N}-{f_s}\) | 0 | 0 |
| ・・・ | ||||
| 9699 | -3.01 | \(\frac{kf_s}{N}-{f_s}\) | 0 | 0 |
| 9700 | -3.00 | \(\frac{kf_s}{N}-{f_s}\) | 0 | 0.5×N |
| 9701 | -2.99 | \(\frac{kf_s}{N}-{f_s}\) | 0 | 0 |
| ・・・ | ||||
| 9799 | -2.01 | \(\frac{kf_s}{N}-{f_s}\) | 0 | 0 |
| 9800 | -2.00 | \(\frac{kf_s}{N}-{f_s}\) | 0.5×N | 0 |
| 9801 | -1.99 | \(\frac{kf_s}{N}-{f_s}\) | 0 | 0 |
| ・・・ | ||||
| 9899 | -1.01 | \(\frac{kf_s}{N}-{f_s}\) | 0 | 0 |
| 9900 | -1.00 | \(\frac{kf_s}{N}-{f_s}\) | 0 | 0.5×N |
| 9901 | -0.99 | \(\frac{kf_s}{N}-{f_s}\) | 0 | 0 |
ちょっと表が長くなったので、共役関係にある部分だけを抽出します。±2Hzも虚部が±0と考えて抽出してみました。
| k | freqs[k] | \(f_k\) | \(α_k\) | \(β_k\) |
|---|---|---|---|---|
| 100 | 1.00 | \(\frac{kf_s}{N}\) | 0 | -0.5×N |
| 9900 | -1.00 | \(\frac{kf_s}{N}-{f_s}\) | 0 | 0.5×N |
| 200 | 2.00 | \(\frac{kf_s}{N}\) | 0.5×N | -0.0 |
| 9800 | -2.00 | \(\frac{kf_s}{N}-{f_s}\) | 0.5×N | +0.0 |
| 300 | 3.00 | \(\frac{kf_s}{N}\) | 0 | -0.5×N |
| 9700 | -3.00 | \(\frac{kf_s}{N}-{f_s}\) | 0 | 0.5×N |
このように、正負の周波数で共役関係になっているのがよくわかると思います。
さて、この辺りで力尽きてしまいました。
当初の目的である任意特性のフィルタを適用するところは次回に回したいと思います。
最後に、作図も含めたPythonのスクリプトを貼り付けておきます。
import os
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.cm as cm
import japanize_matplotlib
from mpl_toolkits.axes_grid1 import make_axes_locatable
#### 関数 ####
# シグナル生成(F:周波数, AS:振幅(sin), AC:振幅(cos), fs:サンプリング周波数, Length:信号長)
def GenSignal(F, AS, AC, fs, Length):
Ts = np.arange(0, Length * 1/fs, 1/fs)
return AS * np.sin(F*Ts*2*np.pi) + AC * np.cos(F*Ts*2*np.pi)
#### 設定事項 ####
N = 10000 #データ長
FS = 100 # サンプリング周波数[Hz]
FF = [1, 2, 3] # 信号の周波数[Hz]
AS = [1, 0, 1] # 振幅_SIN[A.U.]
AC = [0, 1, 0] # 振幅_COS[A.U.]
CONST = 0.5 #直流成分
#### 設定ここまで ####
#シグナル生成(FF:周波数, AS:振幅(Sin), AC:振幅(Cos), fs:サンプリング周波数, Length:信号長)
signal = np.repeat(CONST, N)
for i in range(len(FF)):
signal += GenSignal(FF[i], AS[i], AC[i], FS, N) #周波数:1Hz、サンプリング周波数:100Hz、信号長:N)
#周波数領域に変換
signal_f = np.fft.fft(signal)
freqs = np.fft.fftfreq(N, d=1.0/FS)
# 出力フォルダ
OUT_DIR = "./img01"
# 出力フォルダ生成
if not os.path.exists(OUT_DIR):
os.makedirs(OUT_DIR)
# 波形(時間領域)のグラフ
GRAPH_N = 300
GRAPH_Ts = np.arange(0, GRAPH_N) / FS
plt.figure(figsize=[10.5/2.54, 7.48/2.54])
fig, ax = plt.subplots()
ax.plot(GRAPH_Ts, signal[0:GRAPH_N], label="Signal")
ax.set_xlabel("時刻[s]")
ax.set_ylabel("振幅[A.U.]")
ax.set_title("時間領域(初期の波形;最初の{}データ)".format(GRAPH_N))
fig.tight_layout() #余分な余白削除
plt.savefig("{}/01_時間領域.png".format(OUT_DIR), format="png", dpi=200)
plt.clf()
plt.close()
## 周波数領域のグラフ
fig, ax = plt.subplots(3, 1, figsize=[10.5/2.54, 14.8/2.54])
# 色とラベル
labs = ["絶対値", "実部", "虚部"]
for i in range(3):
ax[i].set_xlabel("周波数")
ax[i].set_ylabel("振幅[A.U.]")
ax[i].set_title("周波数領域(スペクトル・{})".format(labs[i]))
ax[i].set_ylim(-0.6, 0.6)
ax[0].plot(freqs, abs(signal_f) /N, color="black") #絶対値
ax[1].plot(freqs, signal_f.real /N, color="black") #実部
ax[2].plot(freqs, signal_f.imag /N, color="black") #虚部
fig.tight_layout() #余分な余白削除
plt.savefig("{}/02_周波数領域.png".format(OUT_DIR), format="png", dpi=200)
plt.clf()
plt.close()
## 周波数領域のグラフ(低周波部分拡大)
fig, ax = plt.subplots(3, 1, figsize=[10.5/2.54, 14.8/2.54])
# 色とラベル
labs = ["絶対値", "実部", "虚部"]
for i in range(3):
ax[i].set_xlabel("周波数")
ax[i].set_ylabel("振幅[A.U.]")
ax[i].set_title("周波数領域(スペクトル・{})".format(labs[i]))
ax[i].set_xlim(-5, 5) #3Hz以上の成分はないため、5Hz以上は表示していない
ax[i].set_ylim(-0.6, 0.6)
ax[0].plot(freqs, abs(signal_f) /N, color="black") #絶対値
ax[1].plot(freqs, signal_f.real /N, color="black") #実部
ax[2].plot(freqs, signal_f.imag /N, color="black") #虚部
fig.tight_layout() #余分な余白削除
plt.savefig("{}/03_周波数領域(低周波部分拡大).png".format(OUT_DIR), format="png", dpi=200)
plt.clf()
plt.close()