時系列解析というか信号解析で、任意特性のデジタルフィルタを適用したいことがありました。
基礎的な数学の知識も無ければ、Python・NumPyにも不慣れな私が、試行錯誤というか実際に手を動かしてみた結果を、自らの備忘録をかねてとりまとめてみたところです。
フーリエ級数展開
フーリエ変換に入る前に、フーリエ級数展開について触れておきたいと思います。
数学的な正確性を度外視してしまえば、全ての関数\(f(t)\)は三角関数で近似できるというものです1)フーリエ級数|展開の仕組みと計算方法2)フーリエ級数展開の公式と意味|高校数学の美しい物語。
$$ f(t) = \frac{a_{0}}{2}+\sum_{k=1}^{\infty}[a_{k}・cos(kt)+b_{k}・sin(kt)] $$
この式なら、大学レベルの知識の無い私でも理解できました。
さて、この式は複素数の指数関数で表すことが出来ます。
$$ f(t) = \frac{a_{0}}{2}+\sum_{k=-\infty}^{\infty}[c_{k}・exp(-i・t)] $$
三角関数の式では\(0 \leq k \leq \infty\)だったのに対して、複素指数関数表記では\(-\infty \leq k \leq \infty\)となっています。
ちなみに、複素数の指数関数と三角関数はオイラーの公式で繋がっています
$$ exp(z・i)=cos(z)+i・sin(z) $$
NumPyのFFT
さて、ここから本題です。
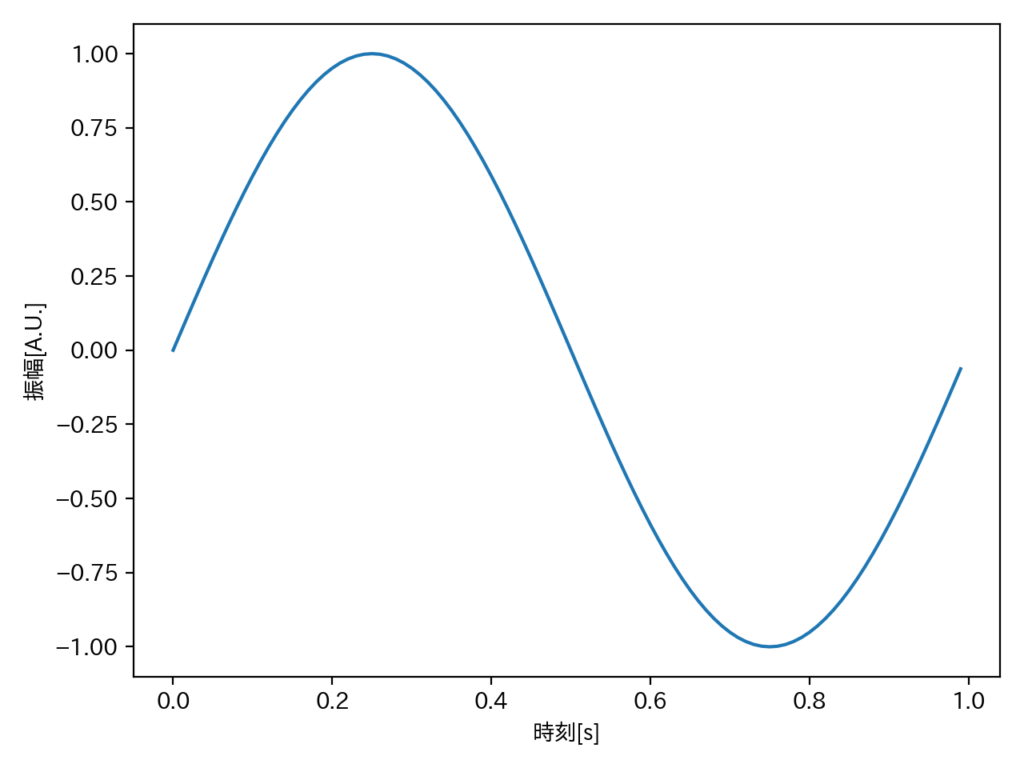
周波数\(F\)のデータ(信号)を考えたいと思います。
$$ f(t) = sin(2πFt) $$
このデータを、データ長:\(N\)、サンプリング周波数:\(f_{s}\)として離散化して、下記のPythonコードで離散フーリエ変換をしてみたいと思います。
できるだけ本文中の記号と、コード中の変数名を合わせようとしていますが、限界がある点はご容赦ください。
import os import numpy as np # サンプルデータ設定 N = 200 #データ長 FS = 100 #サンプリング周波数[Hz] FF = 1 #信号の周波数 ts = np.arange(0, N * 1/FS, 1/FS) #時刻列 signal = np.sin(FF*ts*2*np.pi) #信号列 signal_f = np.fft.fft(signal) #離散フーリエ変換 freqs = np.fft.fftfreq(N, d=1.0/FS) #周波数列
np.fft.fftに信号(時系列データ)を流し込むことで離散フーリエ変換が行われ、時間領域から周波数領域に
離散フーリエ変換の結果はsignal_fに、signal_fに対応する周波数は変数freqsに格納されています。
上記のコードを実行すると、変数「freqs」に周波数が格納されています。この変数「freqs」
実際に格納されている値を見てみましょう。
| k | freqs[k] | \(f_k\) |
|---|---|---|
| 0 | 0.0 | \(\frac{kf_s}{N}\) |
| 1 | 0.5 | \(\frac{kf_s}{N}\) |
| 2 | 1.0 | \(\frac{kf_s}{N}\) |
| ・・・ | ||
| 99 | 49.5 | \(\frac{kf_s}{N}\) |
| 100 | -50.0 | \(\frac{kf_s}{N}-{f_s}\) |
| 101 | -49.5 | \(\frac{kf_s}{N}-{f_s}\) |
| ・・・ | ||
| 198 | -1.0 | \(\frac{kf_s}{N}-{f_s}\) |
| 199 | -0.5 | \(\frac{kf_s}{N}-{f_s}\) |
格納されている値を見ると、0から0.5Hzずつ上がっていった後に、k=100のところで突然-50.0Hzになり、そこから0.5Hzずつ上がっています。
なぜ、k=100のところで、突然-50Hzになるかというと、標本化定理によりサンプリング周波数の半分の周波数(ナイキスト周波数)までしか表現できないということに関係しています。つまり、周波数\(f_k\)の取り得る値は、
$$ -\frac{f_s}{2} \leq f_k \leq \frac{f_s}{2} $$
となります。
さて、FFTの結果「signal_f」の値について踏み込みたいところですが、話が長くなってきたのでいったん筆を置きたいと思います。
続きは↓
[NumPy]FFTでフィルタリング ②離散フーリエ変換
補足
FFTの周波数列について、少し一般化してみました。
ここで、\(M=int(\frac{N}{2})\)とし、「\(int\)」は小数点以下を切り捨てる関数とします。
| k | \(f_k\) |
|---|---|
| \(0\) | \(0\) |
| \(1\) | \(\frac{f_s}{N}\) |
| \(2\) | \(\frac{2f_s}{N}\) |
| ・・・ | |
| \(M-1\) | \(\frac{(M-1)・f_s}{N}\) |
| \(M\) | \(\frac{M・f_s}{N}-f_s\) |
| \(M+1\) | \(\frac{(M+1)・f_s}{N}-f_s\) |
| ・・・ | |
| \(N-2\) | \(\frac{(N-2)・f_s}{N}-f_s\) |
| \(N-1\) | \(\frac{(N-1)・f_s}{N}-f_s\) |