はじめに
2024年8月8日16:43に日向灘で発生したMj7.1(Mw7.0)の地震に伴って、「南海トラフ地震臨時情報(注意情報)」が発表されました。過去にM7クラス以上の地震が発生したあとに、震源の周辺でM8クラス以上の地震が発生した事例があることから、巨大地震への注意を呼びかける目的で発表される情報のようです。
この情報を見ていると、懸念される巨大地震の発生確率について、二つの表現がなされています。
一つ目は、平常時の発生確率と比べて相対的に発生確率が高まっているというものです。
南海トラフ地震関連解説情報(第1号)1)気象庁: 南海トラフ地震関連解説情報(第1号)の中には「南海トラフ地震の想定震源域では、大規模地震の発生可能性が平常時に比べて相対的に高まっていると考えられた」と記載があります。また、南海トラフ沿いの地震に関する評価検討会会長の平田直先生が気象庁で開かれた記者会見で「数倍程度高まっている」という旨の発言をなさっていたかと思います。これが、平常時の発生確率に基づいた相対的な発生確率という事になります。
二つ目は、Mw7.0以上の地震が発生したあとの歴史記録に基づくMw8クラス以上の地震の発生確率です。
気象庁の報道発表資料2)気象庁:令和6年8月8日 16 時 43 分頃の日向灘の地震について(第2報)及び南海トラフ地震関連解説情報(第1号)についてによると、1904~2014年のMw7.0以上の地震が1437回発生していて、そのうち6回でMw8クラス(Mw7.8以上)の地震が1週間以内に6回発生しているそうです。これが、歴史記録に基づくMw8クラス以上の地震の発生確率になります。
ここで、両者の関係に矛盾が無いのかという疑問が湧き上がってきたのが、この記事を書いた目的になります。二つの観点からの地震発生確率の大小関係を把握するために、まずは「平常時」における南海トラフ巨大地震の地震発生確率を、地震調査研究推進本部の長期評価のモデルに準拠して算出したというのがこの記事になります。
長期評価における地震発生確率の算出手法
政府(地震調査研究推進本部)では、過去に発生した南海トラフ巨大地震の発生履歴3)地震調査委員会:南海トラフの地震活動の長期評価(第二版)に基づいて、2024年1月1日からの30年間に南海トラフ巨大地震が発生する確率を70%~80%4)地震調査委員会:長期評価による地震発生確率値の更新について(2024/1/15)と評価しています。
この地震発生確率は、一つ前の地震発生からの経過時間を確率変数とするBPT分布に従うという仮定に基づいて評価されています5)地震調査委員会:長期的な地震発生確率の評価手法について(2001年6月)。BPT分布は物理学においてブラウン運動の初到達時間の分布として導かれたもので、定常的な応力の蓄積による地震発生のモデルと親和性が高いと考えられます。BPT分布は平均発生間隔に相当するμと、発生間隔のばらつきに相当するαの二つのパラメータから構成され、確率密度関数は下記のように表されます。
$$ f(t; μ, α) = \Bigl\{\frac{μ}{2πα^2t^3}\Bigr\}^{1/2}exp\Bigl\{\frac{-(t-μ)^2}{2μα^2t}\Bigr\} $$
確率密度関数というと小難しくてわかりにくいですが、「地震の起こりやすさ」と捉えていただくとわかりやすいかと思います。tが一つ前の地震発生からの経過時間、fが地震の起こりやすさの推移と考えていただくと捉えやすいかと思います。
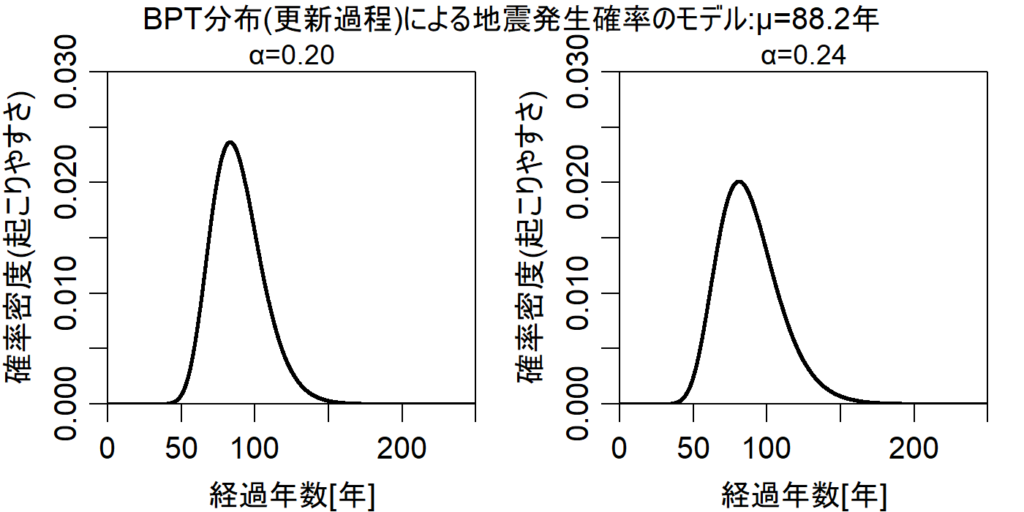
この確率密度関数を、南海トラフ巨大地震の平均発生間隔(μ=88.2年)とばらつき(α=0.20または0.24)に当てはめると、図1のようになります。パラメータαによって若干の違いがあるもののの、一つ前の地震発生(1946/12/21)から40年後くらいまでは確率密度(地震の起こりやすさ)はほぼゼロですが、50年後くらいから上昇し始めて、平均発生間隔88.2年付近でピークに達した後は低下していくという推移です。
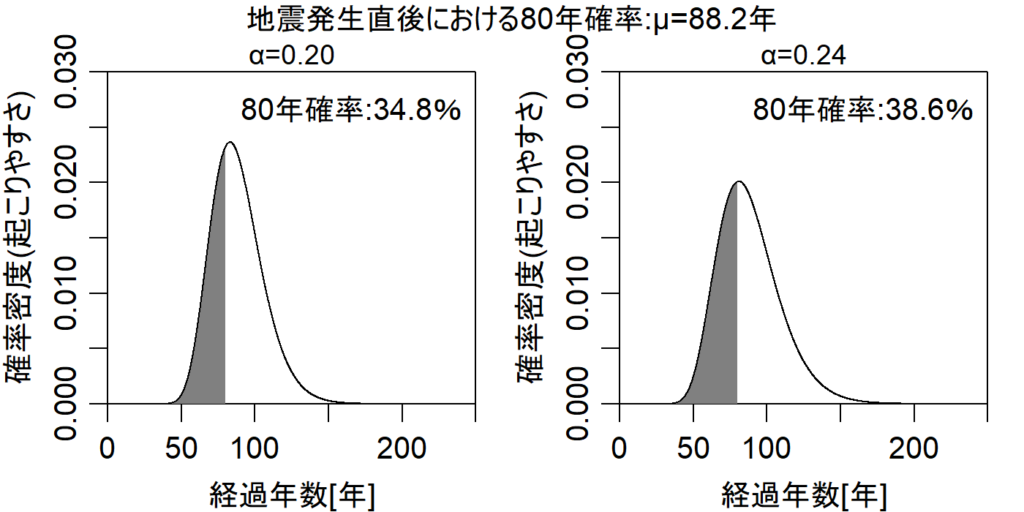
地震発生直後からの地震発生確率は、この確率密度関数を積分することで求められます。積分というと難しそうに思えますが、グラフとX軸で囲まれた面積になります。地震発生直後から80年間の確率を図化すると図2のグレーの部分の面積ということになります。
数式で表すと、一つ前から地震発生直後からT年間の地震発生確率は下記のようになります。
$$ P(T) = \int_0^T f(t; μ, α)dt $$
さて、今は一つ前の地震発生直後ではありません。
一つ前の南海トラフ巨大地震:昭和南海地震(1946/12/21)から令和6年日向灘の地震(2024/8/8)の経過日数は28355日で、1年を365.2425日(グレゴリオス歴の400年平均)とすると、77.63年となります。
現在(2024/8/8)からのT年確率を求める場合には、77.63年地震が発生していなかった事を考慮する必要があります。
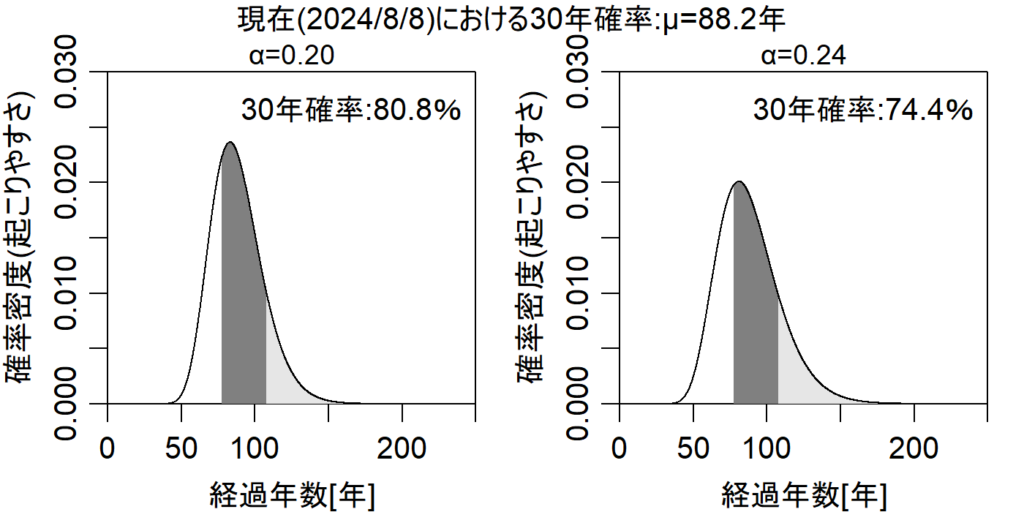
77.63年地震が発生していなかった事を考慮する具体的な方法は、現時点からT年間の発生確率を、現時点から∞までの発生確率で割る事になります。上記を図化すると図3のようになり、濃いグレーの面積を着色部全体の面積(薄いグレーの面積+濃いグレーの面積)で割ることにより現時点からの南海トラフ巨大地震の30年確率を求める事が出来ます。
※修正履歴&謝辞(2024/8/15)
上のパラグラフの表記に誤りがあり修正しました。ご指摘いただいたMamoru Kato(Xアカウント:@mkatolithos)様、ありがとうございました。
一つ前の地震からt年経過(この間に地震は発生していない)した時点から、T年間の地震発生確率を式で表すと下記のようになります。
$$ P(T; t) = \frac{\int_t^{t+T} f(t; μ, α)dt}{\int_t^\infty f(t; μ, α)dt} $$
さて、上記で求めた30年地震発生確率は図3に示した通り、α=0.20の場合は80.8%、α=0.24の場合は74.4となり、地震調査研究推進本部の発表文にある70%~80%と整合していることがわかります。
なお、積分にはRの「integrate」関数を使用する事とします。
7日間発生確率の評価
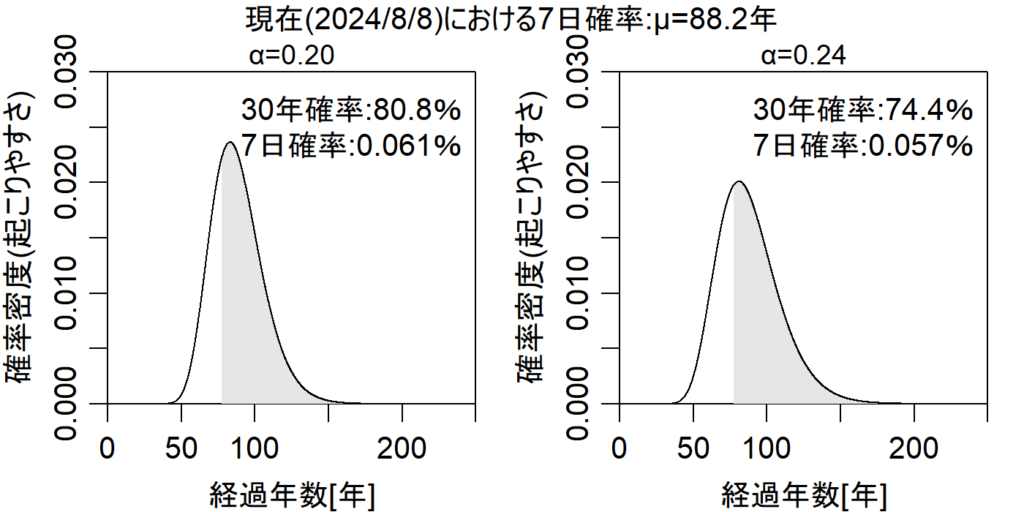
前述の手法に基づいて現時点(2024/8/8)から7日間の南海トラフ巨大地震の発生確率を求めてみたいと思います。1年間を365.2425日とすると7日間は0.019165年となります。これを前述の方法に当てはめた場合の結果を図化すると図4のようになります。なお、7日間が極めて短いため図中では濃いグレーの領域は殆ど見れません。
7日間発生確率をみると概ね0.06%と求められました。
これを分数で表すと1/1667となり、平常時における発生確率になります。
この検討の発端になった「二つの発生確率」を思い出してみましょう。
一つ目は平常時の発生確率と比べて相対的に発生確率が高まっているというものです。数倍を5倍としすると、平常時の確率(1/1667)×5で1/333となります。
二つ目は歴史記録に基づく確率で6/1437(=1/239.5)です。
この二つ(1/333 と 1/239.5)を比較すると矛盾しない結果といえるかと思います。もちろん一致しませんが、桁が合っているどころか、倍半分に収まっているというのはなかなかのものです。
以上より、二つの確率は合っているという結論を得ることが出来ます。
時間予測モデルを用いない場合の発生確率
前述の通り「二つの確率は合っているという結論」を得たのですが、南海トラフ巨大地震の地震発生確率は少し特殊な方法により求められています。具体的には、平均発生間隔に相当するBPT分布のパラメータαが、過去の平均発生間隔と比べると小さいのです。
南海トラフ巨大地震以外の確率は過去に発生した地震の発生間隔からαを求めているのですが、南海トラフ巨大地震は時間予測モデル6)地震調査研究推進本部:時間予測モデルにより求められます。細かい説明は省きますが、ざっくりと一つ前の昭和東南海地震・昭和南海地震のすべり量が小さかったためにαが小さく求められています。
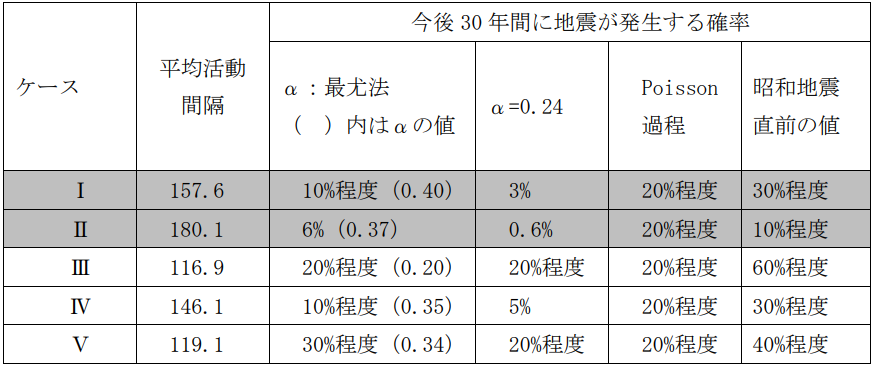
実際の南海トラフ巨大地震の発生履歴に基づくμ・αを使うと地震発生確率が大きく変わります。また、発生履歴についても、古文書記録に基づいていることから、地震を南海トラフ巨大地震と考えるか否かによって複数の考え方があります(表1)7)地震調査委員会:南海トラフの地震活動の長期評価(第二版) p.43(2013.5.24)。
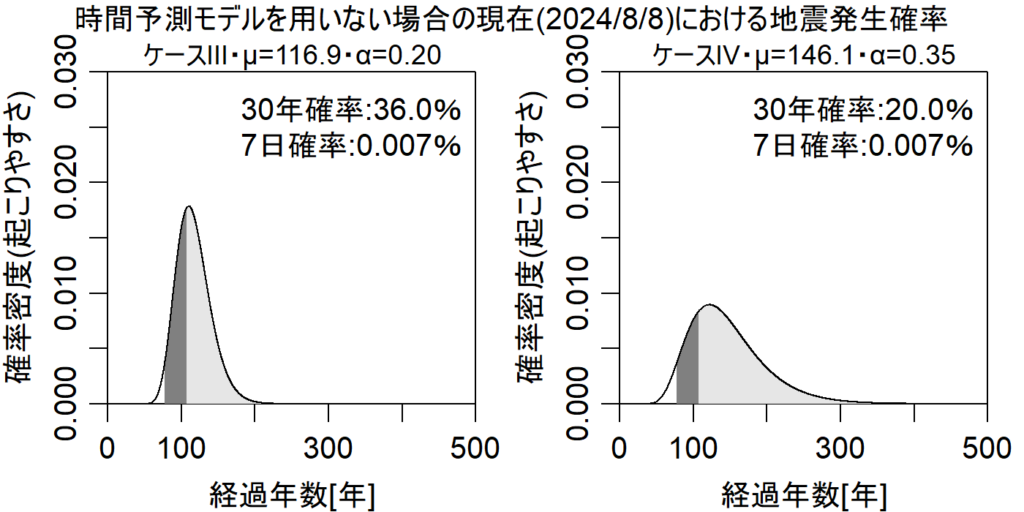
表1のケースⅢ・Ⅳを対象とした時間予測モデルを用いない場合の地震発生確率の算出結果は図5の通りとなります。30年発生確率は20%~36%となり時間予測モデルを用いた場合の半分以下となり、1週間発生確率は0.007%と一桁小さい結果となります。
このように、南海トラフ巨大地震の地震発生確率は、パラメータの考え方によって推定結果が大きく変わります。何千年・何万年の長い時間をかけて多数回の南海トラフ巨大地震を詳細に観測することができればどちらの考え方が妥当なのかが明らかになるかもしれません。しかし、現時点ではどちらの考え方が適切かを評価することは不可能です。
従って、考え方によっては地震発生確率が大きくぶれることを頭に置いた上で意思決定をする必要があるといえます。
まとめ
地震調査研究推進本部の長期評価のモデルに準拠して平常時(日向灘の地震が起こらなかった場合)の1週間地震発生確率を評価すると0.06%程度と求められた。Mw7クラスの地震が発生したあとのMw8クラスの誘発地震の発生確率6/1437(=1/239.5)と比較すると、平常時と比べて確率が上がっていることを加味すれば矛盾しない結果となった。
一方で、長期評価のモデルの前提となっている地震予測モデルを棄却して地震発生確率を求めると、1週間発生確率が一桁程度小さく求められた。
付録: 地震発生確率の推定に用いたスクリプト
rm(list=ls())
setwd("作業ディレクトリ")
#一年あたりの日数
YD <- 1/365.2425
#パラメタ
Mu <- 88.2
dAlpha <- c(0.20, 0.24)
#対象期間
iObsY <- 30
iObsD <- 7
iYrMax <- 250
#経過年数(28355日=1946/12/21~2024/8/8)
dElapseY <- 28355 * YD
## BPT分布の確率密度関数
# https://www.jishin.go.jp/main/choukihyoka/01b/chouki020326.pdf
fnBPT <- function(x){
sqrt(Mu/(2*pi*Alpha^2*x^3))*exp(-(x-Mu)^2/(2*Mu*Alpha^2*x))
}
## グラフ設定 ##
png("fig4_ProbNow1w.png", width=1400, height=700, res=250)
par(mar=c(3, 3, 1, 1)) #余白設定(下、左、上、右)
par(oma=c(0, 0, 1, 0)) #外側余白設定(下、左、上、右)
par(mgp=c(2, 0.7, 0)) #グラフ枠と軸との間隔設定
par(mfrow=c(1, 2)) #グラフ(行×列)
par(xaxs = "i") #データ範囲とグラフの範囲(X軸)
par(yaxs = "i") #データ範囲とグラフの範囲(Y軸)
for(i in 1:length(dAlpha)){
Alpha=dAlpha[i]
# 地震発生確率
dPa <- integrate(fnBPT, dElapseY, Inf)$value #現時点~∞
dP30Y <- integrate(fnBPT, dElapseY, dElapseY+iObsY)$value / dPa
dP07D <- integrate(fnBPT, dElapseY, dElapseY+iObsD*YD)$value / dPa
#作図
plot(NULL, main=sprintf("α=%0.2f", Alpha), font.main=1, cex.main=0.9,
xlim=c(0, iYrMax), xlab="経過年数[年]",
ylim=c(0, 0.03), ylab="確率密度(起こりやすさ)"
)
# 積分範囲
XpgA <- seq(dElapseY, iYrMax, by=0.1)
YpgA <- fnBPT(XpgA)
XpgO <- seq(dElapseY, dElapseY+iObsD*YD, length=10)
YpgO <- fnBPT(XpgO)
polygon(c(dElapseY, XpgA, iYrMax), c(0, YpgA, 0), col=gray(0.9), lty=0)
polygon(c(dElapseY, XpgO, dElapseY+iObsD*YD), c(0, YpgO, 0), col=gray(0.5), lty=0)
# 確率密度関数
dYr <- seq(0, iYrMax, by=0.1)
dDd <- fnBPT(dYr)
lines(dYr, dDd, lty=1, lwd=1)
# 凡例(確率)
labs <- c(
sprintf("%d年確率:%0.1f%", iObsY, 100*dP30Y),
sprintf("%d日確率:%0.3f%", iObsD, 100*dP07D)
)
legend("topright", bty="n", bg="transparent", legend=labs)
}
mtext(sprintf("現在(2024/8/8)における%d日確率:μ=%0.1f年", iObsD, Mu), side=3, outer=T)
dev.off()
脚注
| ↑1 | 気象庁: 南海トラフ地震関連解説情報(第1号) |
|---|---|
| ↑2 | 気象庁:令和6年8月8日 16 時 43 分頃の日向灘の地震について(第2報)及び南海トラフ地震関連解説情報(第1号)について |
| ↑3 | 地震調査委員会:南海トラフの地震活動の長期評価(第二版) |
| ↑4 | 地震調査委員会:長期評価による地震発生確率値の更新について(2024/1/15) |
| ↑5 | 地震調査委員会:長期的な地震発生確率の評価手法について(2001年6月) |
| ↑6 | 地震調査研究推進本部:時間予測モデル |
| ↑7 | 地震調査委員会:南海トラフの地震活動の長期評価(第二版) p.43(2013.5.24) |