モンテカルロシミュレーションとかで、相関を持つ乱数ペアを作りたい場合があるかと思います。ネットを調べると色々と記事が出てくるので作り方の詳細というか、数学的な背景はそちらへ説明を譲るとして、ここでは「こう書いたら出来た」という結論だけを個人的な備忘録として載せておきます。
ちなみに、こちらのコードはこちらを参考にさせて頂きました(謝辞)。
架空データをRで生成する
相関を持った乱数発生
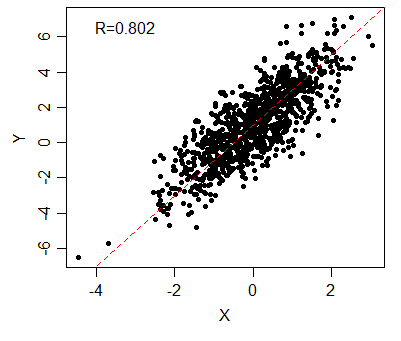
早速、コードと図化してみた結果です。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 | #引数 N:乱数の数、Mu:平均、Sd:標準偏差、R:相関係数#返り値: N行2列の行列(それぞれの列が相関を持つ乱数ペア)CorRand <- function(N, Mu, Sd, R){ x <- rnorm(n=N, mean=Mu, sd=Sd) e1 <- rnorm(n=N, mean=Mu, sd=Sd) e2 <- rnorm(n=N, mean=Mu, sd=Sd) return(cbind(sqrt(R)*x+sqrt(1-R)*e1, sqrt(R)*x+sqrt(1-R)*e2))}#相関を持つ乱数ペア(R=0.8)mt <- CorRand(1000, 0, 1, 0.8)# Y = 1 + 2 * Xx <- mt[,1] #Memo: 関数「CorRand」内とは別物(関数内の変数は外には影響しない)y <- 1 + 2 * mt[,2]#図化:乱数ペアのプロット、破線は回帰直線(Y = 1 + 2 * X)plot(x, y, pch=20, xlab="X", ylab="Y", main="", mgp=c(2, 0.7, 0))legend("topleft", legend=sprintf("R=%0.3f", cor(x, y)), bty="n")lines(c(-5, 5), c(-5*2+1, 5*2+1), lty=2, col=rgb(1,0,0)) |
相関を持つ乱数ペアプロット結果