南岸低気圧による降雪量の不確実性を可視化してみた

はじめに

秋から春にかけての時期に本州の南海上を北東進する南岸低気圧(荒木,2016)¹⁾荒木 健太郎 (2016) 南岸低気圧, 天気, 63, 123-125.は、関東地方にしばしば大雪をもたらし、交通の混乱をはじめとした大きな影響を及ぼす。その一方で、冬季には南岸低気圧による降水が0℃付近の気温で発生することが多いため、気温予想の誤差がわずかであっても積雪量の不確実性が大きくなる特徴がある。そのため、気象庁など気象予報を行う機関では、南岸低気圧に伴う降水現象の予報技術の向上に取り組んでいる(たとえば気象庁予報部(2013)²⁾気象庁予報部 (2013) 日本域拡張・高度化した局地モデルの特性およびガイダンスの高度化, 数値予報解説資料(数値予報研修テキスト), 46など)。
一方で、ユーザー側の立場としては、予想に不確実性を伴っていることを前提とした上で、その不確実性を踏まえて大雪への備えを検討する必要がある。しかしながら、万全の備えには遺失利益を含めて多大なコストがかかるため、適切な程度の備えが必要である。しかしながら、そもそも予測結果の不確実性がどの程度有るのかすらわからない状況では、適切な備えの検討のスタート地点にたつことすら出来ない。
そこで、気温と降水量をインプット情報として、気温・降水量および両者から推定される降雪量予測それぞれの不確実性を確率分布で表現した上で、それぞれの確率分布に従う乱数に基づいてモンテカルロシミュレーションにより、予想される降雪量の不確実性をヒストグラムとハザードカーブ(降雪量と超過確率の関係)で表現した³⁾実のところ、3年ほど前に似たようなことを考えていたものの、考えるべき点が不十分だったので、気温だけでなく、降水量と降雪量予測の不確実性もモデルに加えてみたのです。。

とりあえず結果

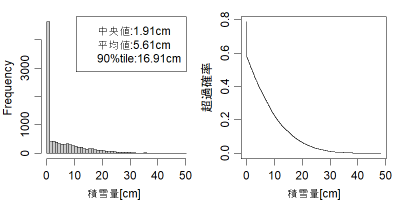
例えば「予想される降水量は(多いところで)10mm、気温は1℃」と予測された場合の降雪量(の不確実性)はこんな感じになります。

図1　シミュレーション結果(降水量10mm&気温1.0℃)

モデルの概要

大雑把に書くと、こんな感じで処理しました。

1. 降水量の不確実性は対数正規分布でモデル化した。
2. 気温の不確実性は正規分布でモデル化した。
3. 過去10年間の観測記録から気温と降水量を説明変数とした回帰式を作成した。
4. 上記の回帰式により降雪量を予測し、回帰式の残差に基づくバラツキを考慮した。

全部をBlogの記事に書こうと思ったのですが、昼休み＆帰宅後の手習いには時間が足らなかったので、とりあえず結果と概要だけをざっくりと書きました。時間があったら、何をやったのかをちゃんと書いてみたいと思います。てか、書き始めたのですが、なんだか論文を書いているような感じになってきて疲れたので断念したという感じです(最初のあたりがそんな書き方になってますね)。

とりあえず、作った図表を脈略も無く貼り付けてみます。

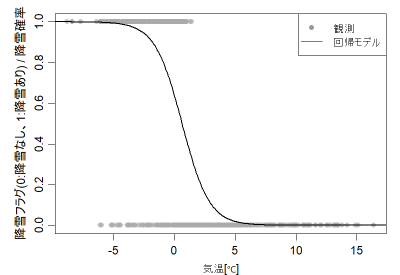
まず、最初に降雪の発生有無を気温からモデル化。

図2 降雪発生の確率モデル(ロジステック回帰分析結果)

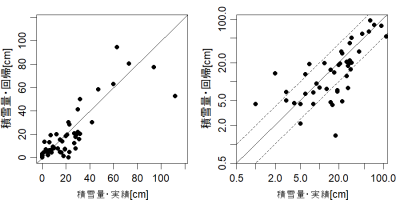
気温と降水量を説明変数とした回帰式⁴⁾実際には図2の降雪発生確率×降水量を説明変数とした。を作って、回帰式による推定結果と実測値を比較。

図3 降水量と気温からの降雪量の推定結果と実測値
左右の違いは軸が線形軸か対数軸かのみ(同じデータ)

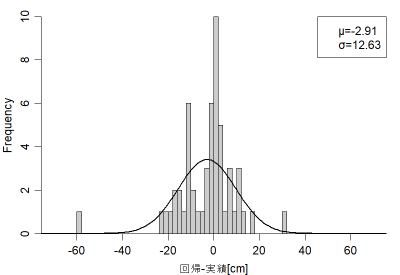
上記の回帰式の予測誤差のヒストグラムと正規分布でモデル化した結果。t分布だととがりすぎるので、とりあえず正規分布を使用した。

図4 降雪量の予測誤差(残差)と誤差のモデル

データの取得対象(事例)。

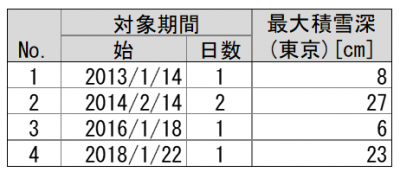
表1 モデルの作成に使用した降雪事例

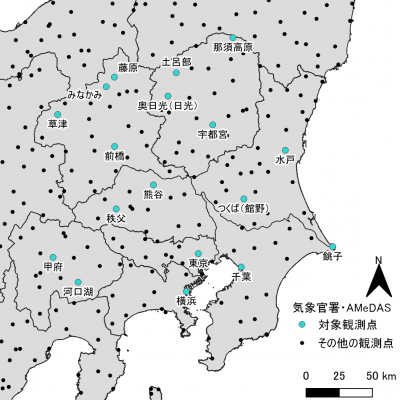
データの取得対象(観測地点)。欠測がある場合は除外した。

図5 データの取得対象としたAMeDAS等の配置