はじめに&謝辞
ちょっと最尤推定(とある分布に従っていると考えている標本から、そのとある分布のパラメータを推定)をしたいことが有ったので、本とかWebなどを調べてみたのですが、私が数学が全然ダメダメということもあって内容が頭に入ってきませんでした。そんな折りに、「【統計学】尤度って何？をグラフィカルに説明してみる。」という記事を拝見して、なんとなく理解できたので、こちらと全く同内容の記事を、自分の備忘録を兼ねてRを使ってリライトしてみたのが今回の内容です。
わかりやすい記事を書いてくださったまつ けん様に感謝申し上げます。
なお冒頭に書いたとおり、数学がダメダメな上に、統計学の基礎も危ういという著者(私)の記事ゆえ、間違っていたり不適切な記載内容の部分もあるかと思います。そんなときは生暖かく見守っていただくか、Twitter等でコッソリご指摘いただければ幸甚です。また、この記載によって得たいかなる損害についても筆者は責任を負わないものとします。
尤度とは
Wikipediaで尤度を調べると下記のように定義されています1)尤度関数 -Wikipedia(2019 Dec.3閲覧)。
尤度関数とは統計学において、ある前提条件に従って結果が出現する場合に、逆に観察結果からみて前提条件が「何々であった」と推測する尤もらしさ（もっともらしさ）を表す数値を、「何々」を変数とする関数として捉えたものである。また単に尤度ともいう。
上記の定義は抽象的なので、「前提条件」を何らかの確率分布、何々とは「パラメータ(μ,σ)の正規分布」、結果を標本と読み替えてみます。
尤度関数とは統計学において、ある確率分布に従って標本が出現する場合に、逆に標本からみて前提条件が「パラメータ(μ,σ)の正規分布」と推測する尤もらしさを表す数値を、パラメータ(μ,σ)を変数とする関数として捉えたものである。
少し具体的になったので、なんとなく頭に入りやすくなったのではないかと思います。この定義(正規分布の場合の例)を頭に入れながら、実際の例に従って計算等を進めてみたいと思います。
正規分布を例に尤度を可視化してみる
前述の正規分布の確率密度関数は、変数をx(パラメータをμ・σ)として下記のように表されます。
$$f(x)=\frac{1}{\sqrt{2\pi\sigma^2}}exp(-\frac{1}{2}\frac{(x-\mu)^2}{\sigma^2})$$
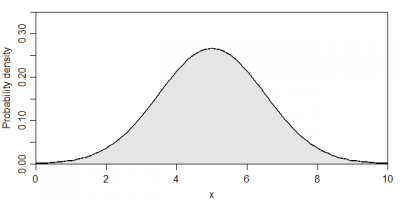
いきなり数式が出てきて頭が痛くなりそうですが、μ=5.0・σ=1.5の場合をグラフに表すと下記のようになります。
正規分布(μ=5.0・σ=1.5)の確率密度
ちなみに、色を塗った部分の面積(
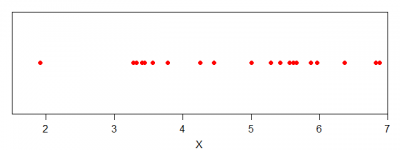
さて、冒頭の定義の部分で「確率分布に従って標本(結果)が出現」とあります。この標本として、μ=5.0・σ=1.5の正規分布に従った乱数を20個発生させます。
setwd("C:/hogehoge/")
#パラメータ
dMu <- 5 #μ
dSd <- 1.5 #σ
dN <- 20 #発生させる乱数の数
#乱数発生
dVal <- rnorm(dN, dMu, dSd)
#プロット
png("00_乱数発生.png", height=240, width=640, res=96)
par(mar=c(3, 1, 1, 1)) #余白設定
par(mgp=c(2, 0.7, 0)) #グラフ枠と軸との間隔設定
par(xaxs = "i") #データ範囲とグラフの範囲(X軸)
plot(dVal, rep(0:0, length=length(dVal)),
ylim=c(-1, 1), xlim=c(1.5, 7) , col="red", pch=16,
xlab="X", ylab="", yaxt="n"
)
dev.off()
発生させた乱数(標本)
標本(結果)から前提条件(母集団の確率分布のパラメータ)を推定する
先ほどは正規分布のパラメータ(μ・σ)を決め打ちさせて乱数(標本)を作成しましたが、ここからは逆のケースを考えます。つまり、正規分布に従って乱数を発生させたことは覚えているものの、パラメータ(μ・σ)を忘れてしまったという状況で手元にある標本からパラメータを推定する場合です。従って、xは定数(標本で既知の値)で、逆に正規分布のパラメータμとσが未知数(変数)となります。
ここで、20個の標本(結果)がこの値となった同時分布を考えてみます。この標本は、Code①の通り同じ分布(正規分布)に基づく乱数で発生させています。つまり、同一の分布から独立に抽出された標本であると考えることが出来るため、同時分布(同時確率密度)はそれぞれの確率密度の積で求めることが出来ます。
$$P(x_{1},x_{2} \cdots x_{20})=P(x_{1}) \times P(x_{2}) \cdots \times P(x_{20})$$
ここで、
$$\begin{align}P(x_{1},x_{2} \cdots x_{20}) &= f(x_{1}) \times f(x_{2}) \cdots \times f(x_{20}) \\
&=\prod_{ i = 0 }^{20} f(x_{i})\\
&=\prod_{ i = 0 }^{20} [ \frac{1}{\sqrt{2\pi\sigma^2}}exp(-\frac{1}{2}\frac{(x_{i}-\mu)^2}{\sigma^2}) ]\end{align}$$
となります。
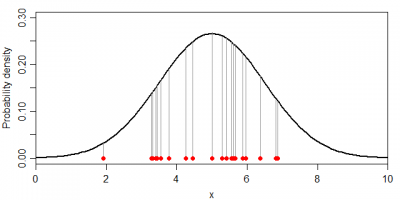
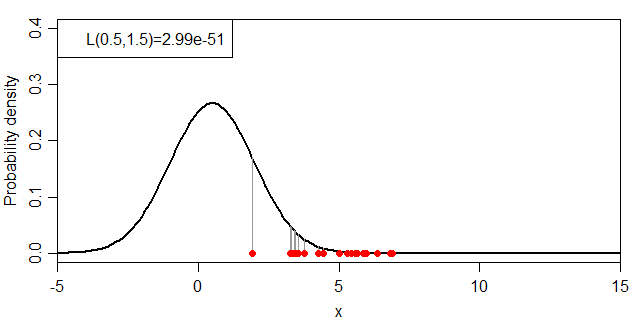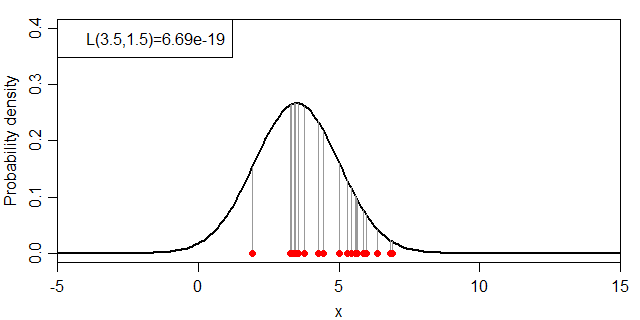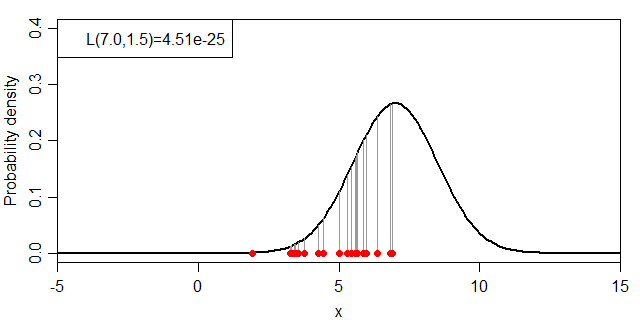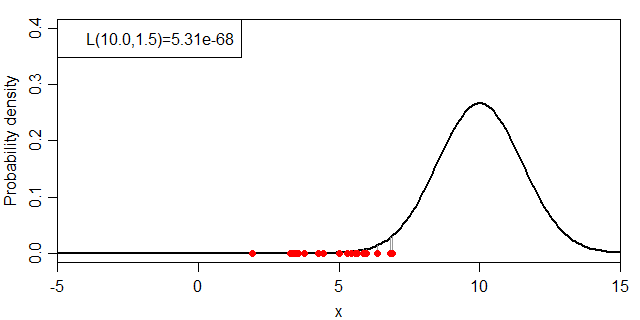
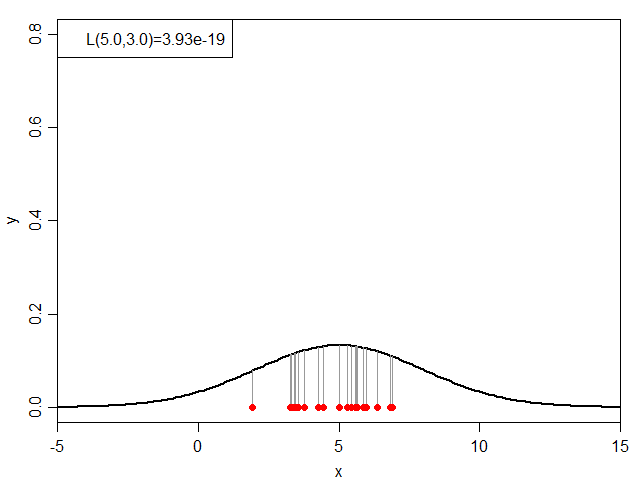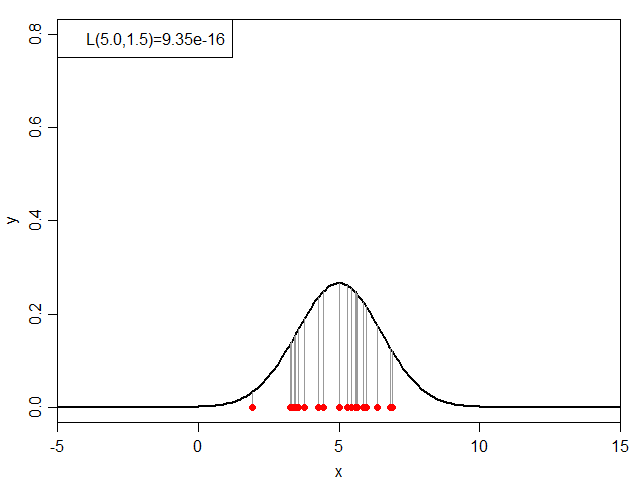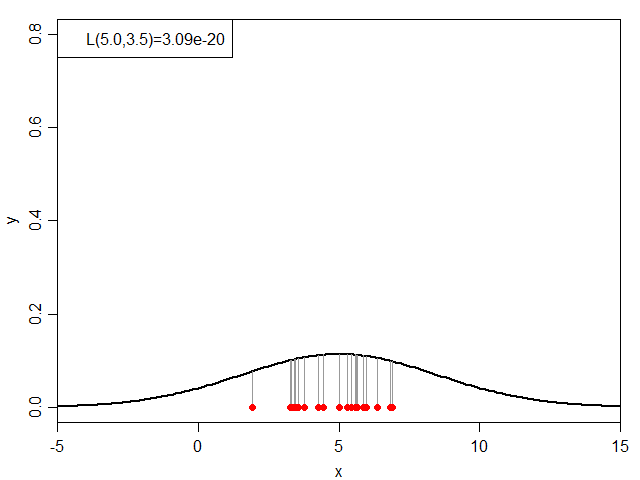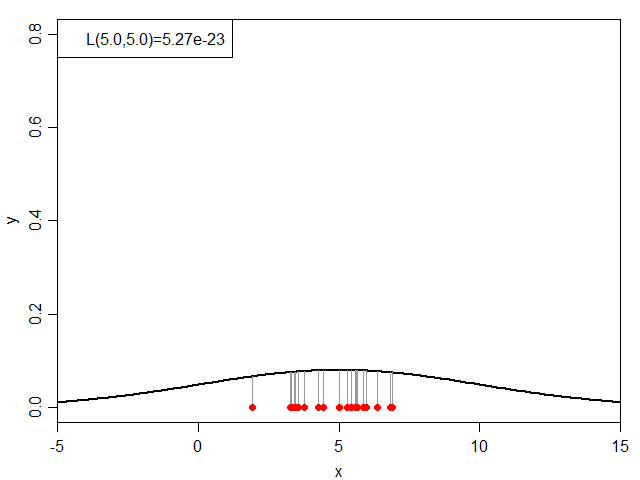
式だと小難しいので絵に表すと、下図のグレーの線の長さの総乗ということになります。
同時分布の計算例
さて、この節の冒頭でxは定数(既知の値)で、逆に正規分布のパラメータμとσが未知数(変数)と書いていました。ここが同時分布と尤度の違いのミソとなるところで、「同時分布はデータの関数であり、尤度は仮定した仮説の関数」2)同時確率分布との違い -Instruction of chemoinformatics(東京大学 化学システム工学専攻 船津研究室)ということになるのです。そこで、関数(右辺)の形は全く同じのまま、変数をμ・σであると宣言し直したものを尤度(Likelihood:L(μ, σ))と下記のように定義します。
$$L(\mu, \sigma)=\prod_{ i = 0 }^{20} [ \frac{1}{\sqrt{2\pi\sigma^2}}exp(-\frac{1}{2}\frac{(x_{i}-\mu)^2}{\sigma^2}) ]$$
それでは、μ・σを変化させた場合に、尤度:L(μ, σ)がどのように変化するかを見ていきましょう。まずは、σを1.5に固定してμを変化させます。
μと尤度(σ=1.5)の関係
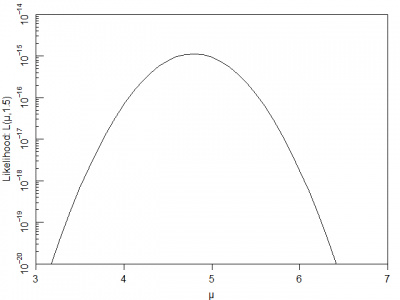
横軸にμ、縦軸にL(μ, σ=1.5)としてグラフにすると下図のようになり、μ=5.0付近で尤度が最大となっています。
μと尤度(σ=1.5)の関係
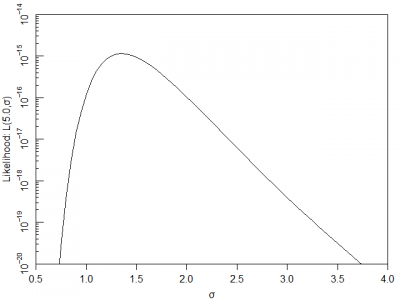
次に、μを5.0に固定した状態でσを変化させてみると下図のようになります。
σと尤度(μ=5.0)の関係
同じく折れ線グラフにすると下図になり、σ=1.5付近で尤度が最大となっています。
σと尤度(μ=5.0)の関係
つまり、尤度:L(μ, σ)が最大となるμとσを探し出すことによって、元の確率分布(のパラメータ)を求めることが出来るということになります。
最適化によりパラメータを推定する
前述の通り尤度:L(μ, σ)が最大となるμとσを探し出せば元の確率分布(のパラメータ)を得ることが出来るのですが、ここで大きな問題が二つあります。
- 尤度の計算がかけ算になっていること。
- ゼロ以上1未満の値を相乗するため非常に小さな値を扱うこととなる(コンピュータで計算した場合に精度が確保できない)。
この問題は尤度の対数を求めることによって克服することが出来ます。この理由は、対数関数が単調増加関数(変数xが増加すれば必ずyも増加する)であること、対数の中身の乗算は対数の加算に置き換えることが出来る(
$$\begin{align}\log L(\mu,\sigma) &= \log [\prod_{ i = 0 }^{n} \frac{1}{\sqrt{2\pi\sigma^2}}exp(-\frac{1}{2}\frac{(x_{i}-\mu)^2}{\sigma^2})]
\\
&= \sum_{ i = 0 }^{n} \log [\frac{1}{\sqrt{2\pi\sigma^2}}exp(-\frac{1}{2}\frac{(x_{i}-\mu)^2}{\sigma^2})]
\end{align}$$
さて、最尤推定の例ではμとσだけが関係する項のみの式に変形してから行うことが一般的3)Rによる最適化、パラメータ推定入門 -yasuhisa’s blogですが、ここでは横着をしてRの組み込み関数である正規分布の確率密度関数(dnorm)をそのまま使って最尤推定してみました。
#対数尤度関数
log_likelihood <- function(x){
return(function(par){
Mu <- par[1]
Sd <- par[2]
return(sum(log(dnorm(x, Mu, Sd))))
})
}
#乱数発生(Code①で発生させた乱数を保持するためベタ打ち)
dVal <- c(3.557094,3.275969,4.458710,5.422027,3.439217,6.876055,5.964535,6.365932,3.322020,3.775108,5.007413,5.665209,5.612997,4.255983,3.408636,5.283933,1.911272,5.562891,5.876041,6.824004)
#rnorm(dN, dMu, dSd)
res <- optim(
par=c(mean(dVal), sd(dVal)),
fn=log_likelihood(dVal),
control=list(fnscale=-1)
)
#結果出力
sprintf("μ=%0.2f", res$par[1])
sprintf("σ=%0.2f", res$par[2])
sprintf("Log[L(μ,σ)]=%0.2f", res$value)
最適化のミソは14行目のoptim関数で、初期パラメータに標本の平均値と標準偏差を入れています。また、optim関数は、デフォルトでは引数(fn)で設定した関数が最小となるように最適化するので、「control=list(fnscale=-1)」で関数が最大となるように設定しています。
最適化の対象となる尤度関数は2～8行目で、xを外側関数が、parを内側関数が受け取る二重関数として定義しています。例えば標本をdVal(11行目で定義)として、μ=1.0・σ=2.0の時の対数尤度を求めたい場合は下記にように実行します。
> log_likelihood(dVal)(c(1.0, 2.0)) [1] -72.67295
上記の実行結果を見ると、μ=4.79、σ=1.34と、「答え」であるμ=5.0、σ=1.5に近い値が得られています。また、対数尤度の最大値は-34.17で、
少し長くなりましたが、様々な分布の確率密度関数を用いることによって、標本から母集団の確率密度のパラメータを求めることが出来る、ということになります。
個人的備忘録(作図等に使用したRのコード)
こちらは、σ=1.5で固定してμを変化させながら尤度を計算しつつ、確率密度関数との関係を示すグラフを連続で作成する。25行目で発生した標本のy=0とy=f(x)を結ぶグレーの線を標本の数だけ書いている。返り値をダミー変数に入れることにより、画面表示を簡潔にしている。
setwd("C:/hogehoge")
#パラメータ
dMu <- 5 #μ
dSd <- 1.5 #σ
dN <- 20 #発生させる乱数の数
#乱数発生(Code①で発生させた乱数を保持するためベタ打ち)
dVal <- c(3.557094,3.275969,4.458710,5.422027,3.439217,6.876055,5.964535,6.365932,3.322020,3.775108,5.007413,5.665209,5.612997,4.255983,3.408636,5.283933,1.911272,5.562891,5.876041,6.824004)
#rnorm(dN, dMu, dSd)
x <- seq(-5, 15, by=0.1)
for(m in 1:20){
dMu_i <- m*0.5
dSd_i <- dSd
png(sprintf("01_尤度_m%0.2d-s%0.2d.png", dMu_i*10, dSd_i*10), height=320, width=640, res=96)
par(mar=c(3, 3, 1, 1)) #余白設定
par(mgp=c(2, 0.7, 0)) #グラフ枠と軸との間隔設定
par(xaxs = "i") #データ範囲とグラフの範囲(X軸)
y <- dnorm(x, dMu_i, dSd_i)
plot(x, y, lty=1, type="l", lwd=2, ylim=c(0, 0.4), xlab="x", ylab="Probability density")
dmy <- sapply(dVal, function(x){lines(c(x, x), c(0, dnorm(x, dMu_i, dSd_i)), col=gray(0.6))})
points(dVal, rep(0:0, length=length(dVal)), col="red", pch=16)
dLH <- prod(dnorm(dVal, dMu_i, dSd_i))
legend("topleft", sprintf("L(%0.1f,%0.1f)=%0.2e", dMu_i, dSd_i, dLH), lty=0)
dev.off()
}
こちらは、σ＝1.5と固定し、μを変化させながら尤度を計算して、尤度:
setwd("C:/hogehoge")
#乱数発生(Code①で発生させた乱数を保持するためベタ打ち)
dVal <- c(3.557094,3.275969,4.458710,5.422027,3.439217,6.876055,5.964535,6.365932,3.322020,3.775108,5.007413,5.665209,5.612997,4.255983,3.408636,5.283933,1.911272,5.562891,5.876041,6.824004)
#rnorm(dN, dMu, dSd)
dMu <- seq(2, 8, by=0.1)
dSd <- 1.5
dL <- sapply(dMu, function(x){prod(dnorm(dVal, x, dSd))})
# グラフ設定
png("①μと尤度(σ=1.5).png", height=480, width=640, res=96)
par(mar=c(3, 3, 1.2, 1)) #余白設定
par(mgp=c(2, 0.7, 0)) #グラフ枠と軸との間隔設定
par(xaxs = "i") #データ範囲とグラフの範囲(X軸)
par(yaxs = "i") #データ範囲とグラフの範囲(Y軸)
# グラフの範囲
iLogL <- -20
iLogU <- -14
plot(dMu, dL, lty=1, type="l", log="y",
xlim=c(3, 7), ylim=c(10^iLogL, 10^iLogU),
xlab="μ", ylab=sprintf("Likelihood: L(μ,%0.1f)", dSd),
yaxt="n", # y軸は後で描く
)
sYlab <- c(expression(10^{-20}),expression(10^{-19}),expression(10^{-18}),expression(10^{-17}),expression(10^{-16}),expression(10^{-15}),expression(10^{-14}))
axis(side=2, #side2:左
at=10^(iLogL:iLogU), #0から8まで1ずつ
tck=0.03, #長さ0.03のティック
labels=sYlab,
mgp=c(1,0.5,0)
)
axis(side=2, #side2:左
at=sapply(iLogL:iLogU, function(x){(2:9)*10^x}), #繰り返し(2:9)×10^(iLogL:iLogU)
tck=0.01, #長さ0.01のティック
labels=FALSE, #ラベル出力なし
mgp=c(1,0.5,0)
)
dev.off()
脚注
| ↑1 | 尤度関数 -Wikipedia(2019 Dec.3閲覧) |
|---|---|
| ↑2 | 同時確率分布との違い -Instruction of chemoinformatics(東京大学 化学システム工学専攻 船津研究室) |
| ↑3 | Rによる最適化、パラメータ推定入門 -yasuhisa’s blog |