[R・お天気]南岸低気圧の雨か雪について考えてみる

関東地方に時々大雪を降らせる南岸低気圧ですが、ちょっと気温の予想がズレただけで雨になったり雪になったりするので、積雪有無(と積雪有りの場合の積雪量)が大きく変わるので(プロの)気象予報士にとって悩みの種というのは有名な話です。

実際にどの程度の誤差が生まれるのか、簡単な仮定に基づいて計算してみました。

＜シミュレーションの仮定＞
• 気温・降水量の予報値と実際の誤差は正規分布に従う
• 気温が0℃未満では降水量1mmあたり1cmの積雪が発生する。
  気温0℃以上では積雪は発生しない。なお、気温は一定で途中で変わらない(気温も雨・雪も)

気温の誤差(の標準偏差)は1.9℃とし、降水量の誤差(の標準偏差)は予想降水量の半分(根拠なし、適当)としました。なお、降水量の予想は20mmとして、気温の予測値を-1.0℃、0℃、1.0℃の3パターン設定します。
なお、負の降水量はあり得ないのでマイナスになる場合に降水量を0mmとしました。

この条件で10000個の気温・降水量を(正規分布に従う)乱数によって作成して、積雪量がどうなるかモンテカルロ的にシミュレーション¹⁾この仮定なら0℃以下の確率を降水量だけから予測した積雪量に乗じれば良かった罠してみました。

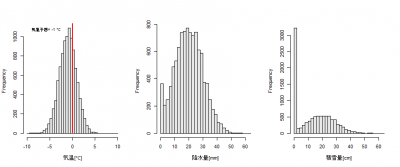
まず、気温予測値が-1.0℃の場合。

気温予想が-1.0℃の場合の気温・降水量・積雪量予想のヒストグラム

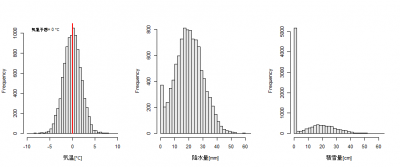
次に、気温予想が0℃の場合。

気温予想が0.0℃の場合の気温・降水量・積雪量予想のヒストグラム

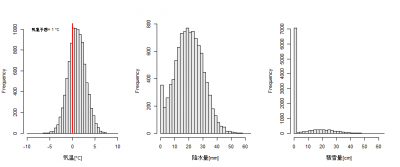
最後に、気温予想が+1.0℃の場合。

気温予想が+1.0℃の場合の気温・降水量・積雪量予想のヒストグラム

雨になるか雪になるか微妙なケースでは、予想される気温によって確率の大小の違いはありますが、ドカ雪になる可能性もありつつ、全く積雪が無い可能性もあるということはおわかり頂けるのではないでしょうか。

実際には、雨になるか雪になるかは湿度の影響も受けますし、積雪するか否かや積雪したときの密度(降水量あたりの積雪量)なんかも様々な要因で変わったり、圧密の影響でΣ降雪量≠積雪量となったりと事は単純ではありません。また、予報誤差が正規分布なのかとか、降水量の誤差は適当に設定しているなどの問題もあります。

さて、今回のヒストグラムを作ったRのスクリプトを最後に貼り付けて…

# 設定
iCn = 10000 #試行回数

dTm = 1 #予想気温
dTs = 1.9 #気温の誤差(RMSE:二乗平均平方根誤差が標準偏差相当とみなした) 
#出典→ http://www.data.jma.go.jp/fcd/yoho/kensho/reimaxt.html

dPm = 20.0 #降水量の予想(mm)
dPs = dPm * 0.5 # 降水量予想の誤差(適当)

par(mfrow=c(1,3)) #縦1×横3に並べる

T <- dTs * rnorm(iCn) + dTm #気温
P <- dPs * rnorm(iCn) + dPm #降水量

dtSnow <- data.frame(気温=T, 降水量=P, 積雪量=rep(0:0, length=iCn))

for(i in 1:iCn){
 if(dtSnow$降水量[i] < 0) dtSnow$降水量[i] <- 0 #降水量にマイナスは無い
 if(dtSnow$気温[i] < 0) dtSnow$積雪量[i] <- dtSnow$降水量[i]
}

#ヒストグラム作図
ht <-hist(
 dtSnow$気温,
 col = "#aaaaaa40",   #ヒストグラムの背景色
 border = "#000000",  #ヒストグラムの境界色
 #ylim=c(0,120),       #y軸の範囲(0～120)
 breaks=seq(-10,10,0.5), #x軸の範囲と間隔(下限、上弦、step)
 main="",          #ヒストグラムのタイトル
 xlab="気温[℃]", #X軸のラベル
 ylab="Frequency"          #Y軸のラベル
)
lines(c(0,0), c(0,1200), col="red", lwd=2, xlim=ht$breaks) #ヒストグラム0℃に赤線
legend("topleft", legend =c(paste(paste("気温予想=", dTm),"℃")), cex = 0.9, bty="n") #グラフ内に文字(予想気温)

hist(
 dtSnow$降水量,
 col = "#aaaaaa40",   #ヒストグラムの背景色
 border = "#000000",  #ヒストグラムの境界色
 #ylim=c(0,120),       #y軸の範囲(0～120)
 breaks=seq(0,65,2), #x軸の範囲と間隔(下限、上弦、step)
 main="",          #ヒストグラムのタイトル
 xlab="降水量[mm]", #X軸のラベル
 ylab="Frequency"          #Y軸のラベル
)

hist(
 dtSnow$積雪量,
 col = "#aaaaaa40",   #ヒストグラムの背景色
 border = "#000000",  #ヒストグラムの境界色
 #ylim=c(0,120),       #y軸の範囲(0～120)
 breaks=seq(0,65,2), #x軸の範囲と間隔(下限、上弦、step)
 main="",          #ヒストグラムのタイトル
 xlab="積雪量[cm]", #X軸のラベル
 ylab="Frequency"          #Y軸のラベル
)