東京の8月の最高気温が期間によって差があるか検定をしようと思ったのですが、まずは分布が正規分布に従っているかを検定しないといけないらしい。
ということで、ヒストグラムと正規確率紙を並べて見るべく、こんなスクリプトを書いてみた。
#ディレクトリ設定(皆様の環境に合わせてください)…ダウンロードしてきたcsvの保存先。
setwd("C:/ほげほげ")
#初期設定
city <- "東京" #観測所名
step <- 15 #1つのヒストグラムの期間
start <- seq(1985,2014,step)
#グラフ設定
par(mfrow=c(1,2)) #縦1×横2に並べる
par(oma = c(2, 0, 0, 0)) #余白設定
#気温データファイルを開く
Temp <- read.csv("東京.csv")
T1 <- Temp[1985 <= Temp$y & Temp$y <= 1999,]
#猛暑日日数をカウントする(T35["TRUE"]に猛暑日(T$max >=35)日数が入る
T35 <- table(T1$max >= 35)
#それぞれのヒストグラムのタイトル(年と猛暑日日数)
title <- paste(i, "~", i+step-1, "年 (猛暑日:", T35["TRUE"], "日)", sep="")
#ヒストグラム作図
hist(
T$max, #最高気温の配列
col = "#aaaaFF40", #ヒストグラムの背景色
border = "#0000AA", #ヒストグラムの境界色
ylim=c(0,120), #y軸の範囲(0~120)
breaks=seq(17,40,1), #x軸の範囲と間隔(17(℃)~40(℃)、1℃刻み)
main=title, #ヒストグラムのタイトル
xlab="最高気温[℃]", #X軸のラベル
ylab="日数" #Y軸のラベル
)
#猛暑日の閾値:35℃に赤い線を引く
lines(c(35,35), c(0,120), col="red", xlim=c(17, 40))
#日数、平均値、中央値を凡例で表示
leg <- c(paste("n =", length(T$max)))
leg <- c(leg, paste("平均値 =", round(mean(T$max), digits = 2)))
leg <- c(leg, paste("中央値 =", round(median(T$max), digits = 2)))
leg <- c(leg, paste("SD=", round(sd(T$max), digits = 2)))
legend("topleft", legend = leg, cex = 0.9, bty="n")
#確率紙プロット
source("http://aoki2.si.gunma-u.ac.jp/R/src/npp2.R", encoding="euc-jp")
npp2(T1$max)
#全体のタイトル
title <- paste(city,"の8月の最高気温")
mtext(title, outer=TRUE, side=1, cex=1.5, line = 0.2)
上のスクリプトを動かすと、こんな感じの絵が描ける。
・・・確率紙があからさまに直線上に並んでいない、曲がっている。
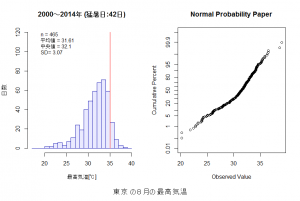
本当に正規分布ではないのか確認するために「Kolmogorov-Smirnov(コロモゴロフ・スミノフ)検定」を行うことにする。Rで「ks.test(引数)」と入力すれば良いのであります。
ということで、コロモゴロフ・スミノフ検定を実行します。
ks.test( #コロモゴロフ・スミノフ検定 T1$max, #データの指定 "pnorm", #正規分布に従っているかを検定 mean=mean(T1$max), #平均 sd=sd(T1$max) #標準偏差 )
するとこんな結果が帰ってきました
One-sample Kolmogorov-Smirnov test data: T1$max D = 0.1, p-value = 2e-05 alternative hypothesis: two-sided Warning message: In ks.test(T1$max, "pnorm", mean = mean(T1$max), sd = sd(T1$max)) : ties should not be present for the Kolmogorov-Smirnov test
手っ取り早く言うと、4行目のp-valueがとっても小さいということ(p < 0.05) なので「データ(2000~2014年の8月の東京の最高気温)が正規分布をなす」という帰無仮説が棄却される事になります。 ということで、一般的によく使われているt検定は使えなさそうということが分かりました。 なのでノンパラメトリック検定で、東京の平均気温が年代によって変わるのかを確かめることになりそうです。 続く・・・のか?
参考:Rでt検定 2(帯広畜産大学 増田豊 研究室のWebサイト)