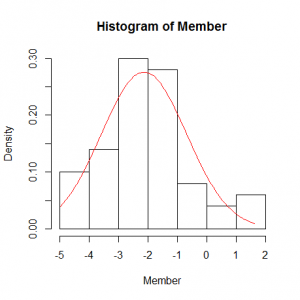
標本値を元に、母集団が正規分布に従うと仮定した場合のパラメータを推定して、推定した正規分布の曲線を標本値の棒グラフの上に重ねようというもの。
最尤法によるパラメータ推定やグラフを描く解説はあちらこちらに有るのですが、自分のやりたかったことを一発で解説しているところが無かったので、未来の私に向けてへのメモをかねて。
さっそく、コードを↓に貼り付けてと。
#▼最尤推定
#対数尤度関数
log_likelihood_for_norm <- function(x){
return(function(par){
mu <- par[1]
sigma2 <- par[2]
- length(x) / 2 * log(sigma2) - 1 / 2 * sum((x - mu)^2) / sigma2
})
}
#乱数発生
Member <- rnorm(50, mean=-2, sd=1.5)
#最尤推定
opt <- optim(par = c(-3, 1), fn = log_likelihood_for_norm(Member), control = list(fnscale = -1))
M <- opt$par[1]
S <- sqrt(opt$par[2])
#グラフを描く
hist(Member, freq=F)
step <- seq(min(Member), max(Member), 0.1)
lines(step, dnorm(step, M, S), col="red", xlim=c(min(Member), max(Member)))
まず1~9行目。
これは、最尤法でパラメータを推定するための(対数)尤度関数。
ここで求められる尤度が最大になるようにRで推定してもらいます。
12行目
ここで、標本を発生させています。
平均-2、標準偏差1.5の正規分布に従う乱数を50個発生させています。
15行目
12行目で発生させた乱数を標本として、母集団のパラメーターを推定しています。
推定結果(optim関数の結果)が変数optに入るようにしています。
そして、16・17行目で平均と標準偏差を取り出しています。
19行目
標本のヒストグラムを描いています。第二引数「freq=F」で縦軸を密度にしています。
20行目
標本の最小値から最大値まで、0.1刻みの数を変数(配列)「step」に入れています(折れ線グラフを描くため)
21行目
20行目で発生させたstepを元に、正規分布の折れ線グラフを描いています。
引数①でstep:0.1刻み
引数②で0.1刻みに、平均M・標準偏差Sの正規分布のグラフを描かせています。
引数③で線の色を指定
引数④でX軸の範囲を指定しています。
このBlogを書くに当たって(主に)下記のサイトの情報を参考にさせて頂きました。
・[R]Rによる最適化、パラメータ推定入門
・Rでヒストグラムを書いて正規分布曲線と重ねる