前回まで、NumPyのFFTで得られる結果と周波数について話してきました。
今回は、任意特性のフィルタを適用して目的の周波数(帯)の信号を取り出してみたいと思います。
やりたいこと(目的)
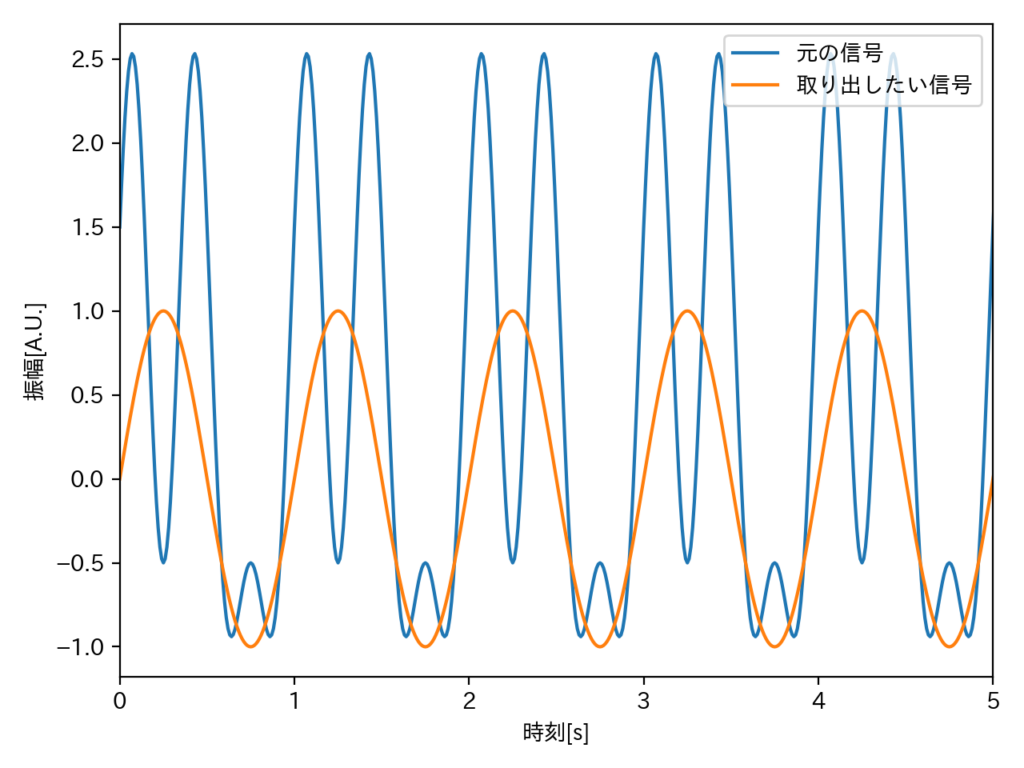
端的に言えば、下記の青い曲線(信号・波形)から、橙色の曲線を取り出したいというものです。
元の信号
複数周期・位相の三角関数により表された信号です。具体的には下記の三角関数により表されます。
$$ f(t) = 0.5 + sin(2πt) + cos(4πt) + sin(6πt) $$
この式をフーリエ級数展開の式に当てはめるとこのように表せます。
$$ f(t) = \frac{a_{0}}{2}+\sum_{m=1}^{3}[a_{m}cos(2πmt)+b_{m}sin(2πmt)] $$
| \(m[Hz]\) | \(a_m\) | \(b_m\) |
|---|---|---|
| 0 | 1 | – |
| 1 | 1 | 0 |
| 2 | 0 | 1 |
| 3 | 1 | 0 |
取り出したい信号
上記のうち、周波数1Hzの信号を取り出したい信号とします。
$$ f(t) = sin(2πt) $$
フィルタの設計
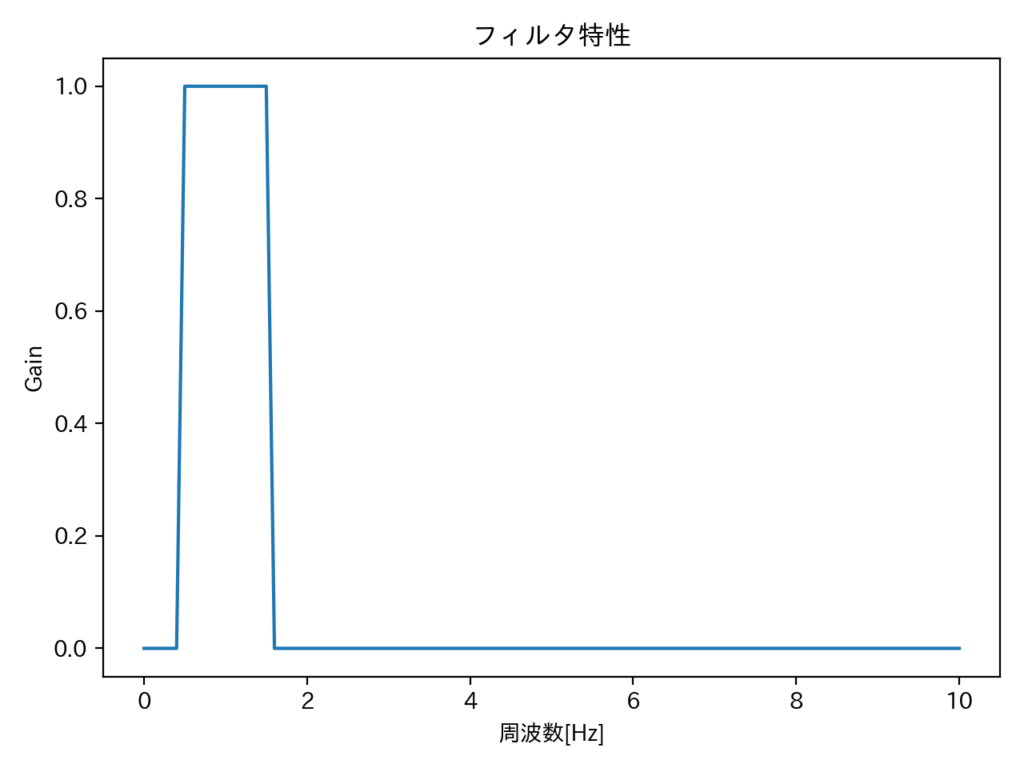
目的を達成するためには周波数1Hzを通し(ゲイン:1)、周波数2Hz・3Hzを通さない(ゲイン:0)フィルタであれば何でも良いのですが、ここでは周波数0.5Hzから1.5Hzのみを通すバンドパスフィルタを使用する事とします。
周波数特性は下図のようになります。
一般的にデジタルフィルタといえばバタワース型とか色々ありますが、それらとは全然違うというか、恣意的な特性です。なお、位相特性とかありますが、ここでは考えていません。
ちなみに、Pythonでは任意の周波数を入れると利得(ゲイン)を返す下記の関数で実装しました。ここで、周波数の絶対値をとっているのは、負の周波数(前々回参照)が入ってきたときに、正の周波数のゲインを返すための処理です。
# 任意フィルタ(周波数が0.5~1.5Hzの時のみ通す) def Freq2Gain(F): if 0.5 <= abs(F) and abs(F) <= 1.5: return(1) else: return(0)
フィルタの適用
フィルタの適用は至って簡単です。
周波数空間の複素スペクトルに、フィルタ特性に基づくゲインを乗じているだけです。
最後に、逆フーリエ変換(IFFT)して時間空間(波形)に戻すだけです。
## 周波数領域に変換 signal_f = np.fft.fft(signal) freqs = np.fft.fftfreq(N, d=1.0/FS) ## フィルタ適用 filterd_f = np.zeros(len(signal_f), dtype=np.complex64) for i in range(len(signal_f)): filterd_f[i] = signal_f[i].real * Freq2Gain(freqs[i]) + 1j*signal_f[i].imag * Freq2Gain(freqs[i]) ## 周波数領域→時間領域 filterd = np.fft.ifft(filterd_f)
ここで、複素スペクトルの各要素にフィルタの利得(ゲイン)を乗しています。
これ、ものすごく効率が悪いです。
波形を一つだけ処理するのであれば、現代の計算機では問題ないのですが、多数の波形を処理する場合にはあまりにも効率が悪いです。
あらかじめ、ゲインをベクトルにしておいて、ベクトル同士で掛けた方が効率的です。
## 周波数領域に変換 signal_f = np.fft.fft(signal) freqs = np.fft.fftfreq(N, d=1.0/FS) ## ゲインのベクトル gains = np.zeros(len(freqs)) for i in range(len(freqs)): gains[i] = Freq2Gain(freqs[i]) ## フィルタ適用 filterd_f = signal_f * gains ## 周波数領域→時間領域 filterd = np.fft.ifft(filterd_f)
フィルタを適用した波形
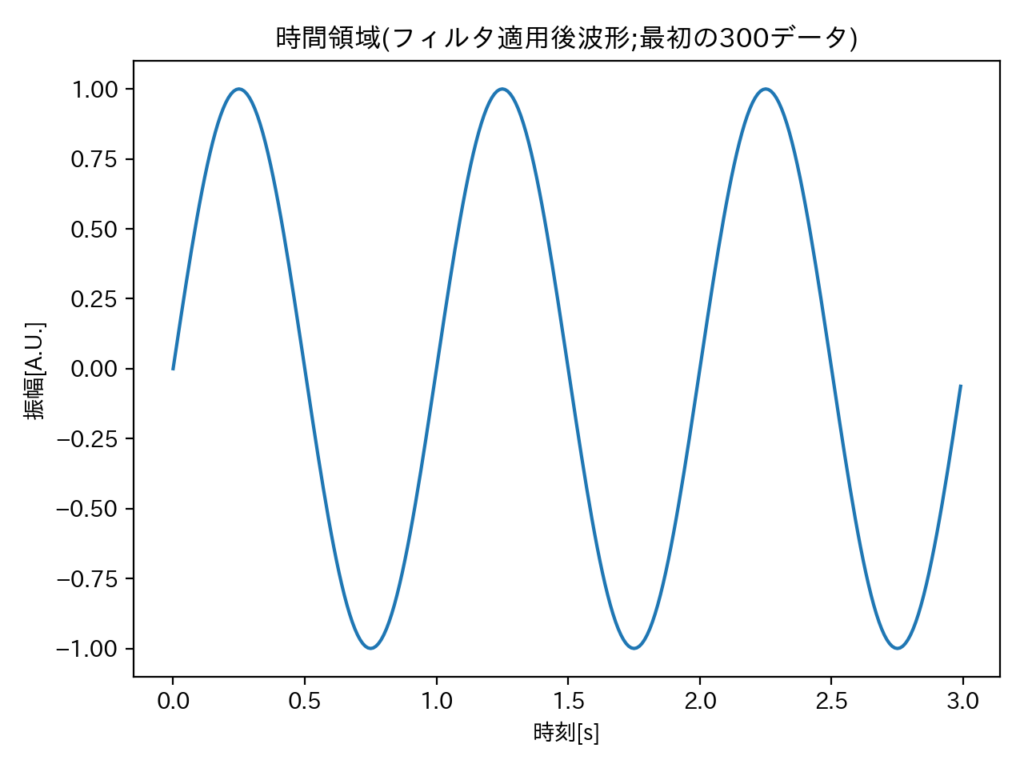
前項によりバンドパスフィルタを適用した波形は下記に示した通りです。
見事に周期1秒、振幅1のサインカーブを取り出すことが出来ました。
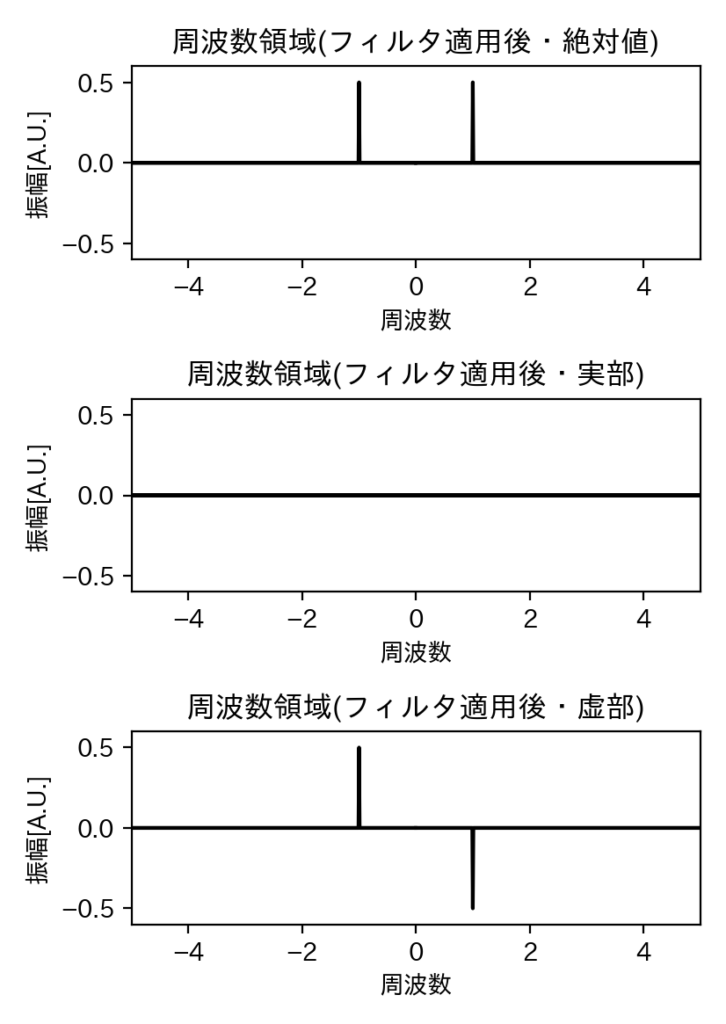
ちなみに、波形に戻す前の複素スペクトルは下記の通りです。
当たり前といえば当たり前ですが、周期1秒以外のスペクトルは完全にカットされています。
まとめ
三回に分けてフーリエ級数展開から、Python(NumPy)のFFTの結果について周波数を中心に結果の見方を確認したうえで、任意特性のフィルタを適用してみました。
フィルタの位相特性などは割愛、というか理解が追いついていない部分があるのですが、ひとまずこの方法で任意特性のフィルタを作成するとともに、任意特性のフィルタを適用して目的の信号を取り出すことが出来ました。
記事作成に使用したコード(Python・NumPy)
この手の解説記事だと、通しで動くプログラムが公開されていないことが多いようです。
それで、非常につまらない部分で時間を費やすことがあったりします。
(切り取ったコードに間違えがある場合など)。
ということで、将来の自分自身へ向けて、少なくとも記事を書いたときには動いたプログラムを末尾に貼っています。
import os
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.cm as cm
import japanize_matplotlib
from mpl_toolkits.axes_grid1 import make_axes_locatable
#### 関数 ####
# シグナル生成(F:周波数, AS:振幅(sin), AC:振幅(cos), fs:サンプリング周波数, Length:信号長)
def GenSignal(F, AS, AC, fs, Length):
Ts = np.arange(0, Length * 1/fs, 1/fs)
return AS * np.sin(F*Ts*2*np.pi) + AC * np.cos(F*Ts*2*np.pi)
# 任意フィルタ(周波数が0.5~1.5Hzの時のみ通す)
def Freq2Gain(F):
if 0.5 <= abs(F) and abs(F) <= 1.5:
return(1)
else:
return(0)
#### 設定事項 ####
N = 10000 #データ長
FS = 100 # サンプリング周波数[Hz]
FF = [1, 2, 3] # 信号の周波数[Hz]
AS = [1, 0, 1] # 振幅_SIN[A.U.]
AC = [0, 1, 0] # 振幅_COS[A.U.]
CONST = 0.5 #直流成分
#### 設定ここまで ####
# シグナル生成(FF:周波数, AS:振幅(Sin), AC:振幅(Cos), fs:サンプリング周波数, Length:信号長)
signal = np.repeat(CONST, N)
for i in range(len(FF)):
signal += GenSignal(FF[i], AS[i], AC[i], FS, N) #周波数:1Hz、サンプリング周波数:100Hz、信号長:N)
## 周波数領域に変換
signal_f = np.fft.fft(signal)
freqs = np.fft.fftfreq(N, d=1.0/FS)
## フィルタ特性(利得のベクトル)
gains = np.zeros(len(freqs))
for i in range(len(freqs)):
gains[i] = Freq2Gain(freqs[i])
## フィルタ適用
filterd_f = signal_f * gains
## 周波数領域→時間領域
filterd = np.fft.ifft(filterd_f)
#### ここから作図用コード ####
# 出力フォルダ生成
OUT_DIR = "./img03"
if not os.path.exists(OUT_DIR):
os.makedirs(OUT_DIR)
# 波形(時間領域)のグラフ
GRAPH_N = 300
GRAPH_Ts = np.arange(0, GRAPH_N) / FS
plt.figure(figsize=[10.5/2.54, 7.48/2.54])
fig, ax = plt.subplots()
ax.plot(GRAPH_Ts, signal[0:GRAPH_N], label="Signal")
ax.set_xlabel("時刻[s]")
ax.set_ylabel("振幅[A.U.]")
ax.set_title("時間領域(初期の波形;最初の{}データ)".format(GRAPH_N))
fig.tight_layout() #余分な余白削除
plt.savefig("{}/01_時間領域.png".format(OUT_DIR), format="png", dpi=200)
plt.clf()
plt.close()
## 周波数領域のグラフ
fig, ax = plt.subplots(3, 1, figsize=[10.5/2.54, 14.8/2.54])
# 色とラベル
labs = ["絶対値", "実部", "虚部"]
for i in range(3):
ax[i].set_xlabel("周波数")
ax[i].set_ylabel("振幅[A.U.]")
ax[i].set_title("周波数領域(スペクトル・{})".format(labs[i]))
ax[i].set_ylim(-0.6, 0.6)
ax[0].plot(freqs, abs(signal_f) /N, color="black") #絶対値
ax[1].plot(freqs, signal_f.real /N, color="black") #実部
ax[2].plot(freqs, signal_f.imag /N, color="black") #虚部
fig.tight_layout() #余分な余白削除
plt.savefig("{}/02_周波数領域.png".format(OUT_DIR), format="png", dpi=200)
plt.clf()
plt.close()
## 周波数領域のグラフ(長周期部分拡大)
fig, ax = plt.subplots(3, 1, figsize=[10.5/2.54, 14.8/2.54])
# 色とラベル
labs = ["絶対値", "実部", "虚部"]
for i in range(3):
ax[i].set_xlabel("周波数")
ax[i].set_ylabel("振幅[A.U.]")
ax[i].set_title("周波数領域(スペクトル・{})".format(labs[i]))
ax[i].set_xlim(-5, 5)
ax[i].set_ylim(-0.6, 0.6)
ax[0].plot(freqs, abs(signal_f) /N, color="black") #絶対値
ax[1].plot(freqs, signal_f.real /N, color="black") #実部
ax[2].plot(freqs, signal_f.imag /N, color="black") #虚部
fig.tight_layout() #余分な余白削除
plt.savefig("{}/03_周波数領域(低周波部分拡大).png".format(OUT_DIR), format="png", dpi=200)
plt.clf()
plt.close()
## フィルタ特性表示
GRAPH_Fs = np.arange(0, 10.1, 0.1)
GRAPH_Gs = np.zeros(len(GRAPH_Fs))
for i in range(len(GRAPH_Fs)):
GRAPH_Gs[i] = Freq2Gain(GRAPH_Fs[i])
plt.figure(figsize=[10.5/2.54, 7.48/2.54])
fig, ax = plt.subplots()
ax.plot(GRAPH_Fs, GRAPH_Gs, label="Gain")
ax.set_xlabel("周波数[Hz]")
ax.set_ylabel("Gain")
ax.set_title("フィルタ特性")
fig.tight_layout() #余分な余白削除
plt.savefig("{}/04_フィルタ特性.png".format(OUT_DIR), format="png", dpi=200)
plt.clf()
plt.close()
## フィルタ適用後・周波数領域のグラフ(長周期部分拡大)
fig, ax = plt.subplots(3, 1, figsize=[10.5/2.54, 14.8/2.54])
# 色とラベル
labs = ["絶対値", "実部", "虚部"]
for i in range(3):
ax[i].set_xlabel("周波数")
ax[i].set_ylabel("振幅[A.U.]")
ax[i].set_title("周波数領域(フィルタ適用後・{})".format(labs[i]))
ax[i].set_xlim(-5, 5)
ax[i].set_ylim(-0.6, 0.6)
ax[0].plot(freqs, abs(filterd_f) /N, color="black") #絶対値
ax[1].plot(freqs, filterd_f.real /N, color="black") #実部
ax[2].plot(freqs, filterd_f.imag /N, color="black") #虚部
fig.tight_layout() #余分な余白削除
plt.savefig("{}/05_フィルタ適用後スペクトル(低周波部分拡大).png".format(OUT_DIR), format="png", dpi=200)
plt.clf()
plt.close()
# 波形(時間領域)のグラフ
plt.figure(figsize=[10.5/2.54, 7.48/2.54])
fig, ax = plt.subplots()
ax.plot(GRAPH_Ts, filterd[0:GRAPH_N], label="Signal")
ax.set_xlabel("時刻[s]")
ax.set_ylabel("振幅[A.U.]")
ax.set_title("時間領域(フィルタ適用後波形;最初の{}データ)".format(GRAPH_N))
fig.tight_layout() #余分な余白削除
plt.savefig("{}/06_フィルタ適用後波形.png".format(OUT_DIR), format="png", dpi=200)
plt.clf()
plt.close()